×
![]()
neos-pseudoapplication-95
| Type: | Model Group |
| Submitter: | NEOS Server Submission |
| Description: | Imported from the MIPLIB2010 submissions. |
Parent Model Group (neos-pseudoapplication-95)
All other model groups below were be compared against this "query" model group.  |
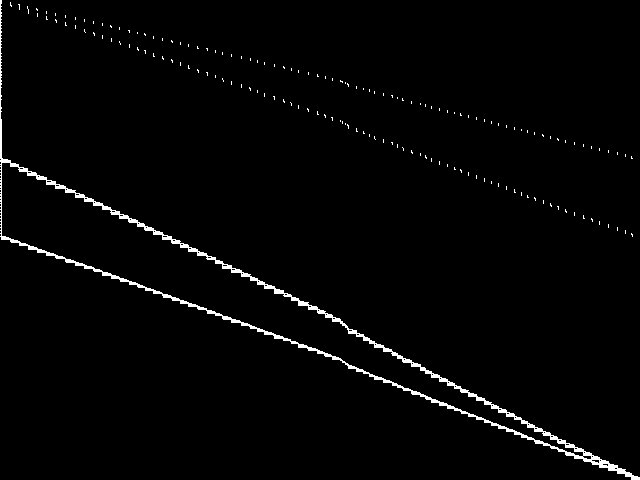 |
|
Model Group Composite (MGC) image
Composite of the decomposed CCM images for every instance in the query model group.
|
Component Instances (Decomposed)
These are the decomposed CCM images for each instance in the query model group.  |
These are component instance images.
|
 |
 |
 |
 |
 |
| Name | neos-827015 | neos-829552 |
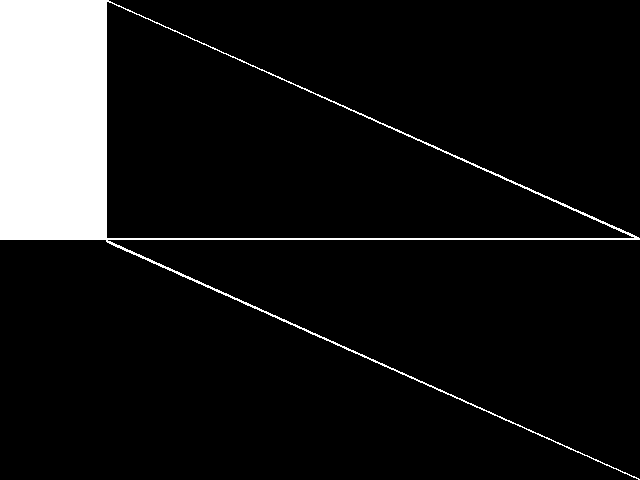
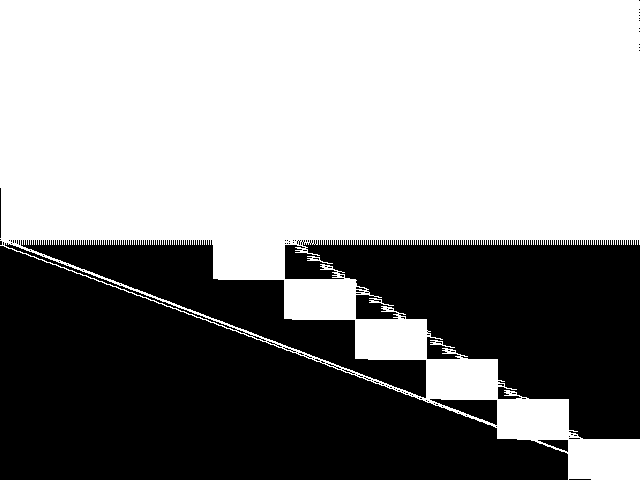
MIC Top 5 Model Groups
These are the 5 MGC images that are most similar to the MGC image for the query model group, according to the ISS metric.  |
FIXME - These are model group composite images.
|
 |
 |
 |
 |
 |
| Name | 8div | neos-pseudoapplication-77 | neos-pseudoapplication-74 | pegsolitaire | rpp | |
|
Rank / ISS
The image-based structural similarity (ISS) metric measures the Euclidean distance between the image-based feature vectors for the query model group and all other model groups. A smaller ISS value indicates greater similarity.
|
1 / 1.521 | 2 / 1.662 | 3 / 1.673 | 4 / 1.677 | 5 / 1.801 |
Model Group Summary
The table below contains summary information for neos-pseudoapplication-95, and for the five most similar model groups to neos-pseudoapplication-95 according to the MIC.
| MODEL GROUP | SUBMITTER | DESCRIPTION | ISS | RANK | |
|---|---|---|---|---|---|
| Parent Model Group | neos-pseudoapplication-95 | NEOS Server Submission | Imported from the MIPLIB2010 submissions. | 0.000000 | - |
| MIC Top 5 | 8div | Sascha Kurz | Projective binary 8-divisible linear block codes A linear block code is called 8-divisible if the weights of its codewords are divisible by 8. It is called projective if there are no duplicate columns in the generator matrix. The possible lengths of 8-divisible linear block codes have been classified except for length n=59, where it is undecided whether such a linear code exists. The possible dimensions satisfy \\(10 \\le k \\le 20\\). Model 8div_n59_kXX contains the corresponding feasibility problem. Projective binary 8-divisible linear block codes occur as hole configurations of so-called partial solid spreads in finite geometry. Binary 4-divisible linear block codes have applications in physics. | 1.521255 | 1 |
| neos-pseudoapplication-77 | Jeff Linderoth | (None provided) | 1.661527 | 2 | |
| neos-pseudoapplication-74 | Jeff Linderoth | (None provided) | 1.673055 | 3 | |
| pegsolitaire | Hiroshige Dan | Model to solve model of a board game "Peg solitaire" | 1.677321 | 4 | |
| rpp | Gleb Belov | These are the models from MiniZinc Challenges 2012-2016 (see www.minizinc.org), compiled for MIP WITH INDICATOR CONSTRAINTS using the develop branch of MiniZinc and CPLEX 12.7.1 on 30 April 2017. Thus, these models can only be handled by solvers accepting indicator constraints. For models compiled with big-M/domain decomposition only, see my previous submission to MIPLIB.To recompile, create a directory MODELS, a list lst12_16.txt of the models with full paths to mzn/dzn files of each model per line, and say$> ~/install/libmzn/tests/benchmarking/mzn-test.py -l ../lst12_16.txt -slvPrf MZN-CPLEX -debug 1 -addOption "-timeout 3 -D fIndConstr=true -D fMIPdomains=false" -useJoinedName "-writeModel MODELS_IND/%s.mps" Alternatively, you can compile individual model as follows: $> mzn-cplex -v -s -G linear -output-time ../challenge_2012_2016/mznc2016_probs/zephyrus/zephyrus.mzn ../challenge_2012_2016/mznc2016_p/zephyrus/14__8__6__3.dzn -a -timeout 3 -D fIndConstr=true -D fMIPdomains=false -writeModel MODELS_IND/challenge_2012_2016mznc2016_probszephyruszephyrusmzn-challenge_2012_2016mznc2016_probszephyrus14__8__6__3dzn.mps | 1.801131 | 5 |

