×
![]()
Model Groups
This analysis, referred to as the MIPLIB Image Comparison (MIC) considers 992 of the instances in MIPILB 2017. Of these, 783 were assigned by MIPLIB to one of 238 model groups. These model groups are listed here. For each model group the submitter, description, and number of member instances are provided.
In addition to descriptive information, the model group composite (MGC) images are shown for each model group. An MGC image is a composite (or overlay) of the constraint coefficient matrix (CCM) images for each instance which belongs to the corresponding model group.
Click on any model group name to see a subset of the MIC's model-to-model comparison results for that group.
Available Model Groups
| COMPOSITE OF MEMBER INSTANCE IMAGES | ||||||
|---|---|---|---|---|---|---|
| MODEL GROUP | SUBMITTER | DESCRIPTION | Num. Instances | Zeros are Black | Zeros are White | |
| 1 | 2hopcds | Austin Buchanan | A problem in wireless networks. The objective is to select a minimum number of relay nodes so that any two nonadjacent nodes can communicate by way of the chosen relay nodes in at most s hops, where s is a problem input. The 2-hop case of this problem can be formulated as a set cover/hitting set problem with n binary variables and n^2 constraints: _{ k N(i) N(j) } x_k 1 for nonadjacent node pairs {i,j}. Despite the formulation's simplicity, models with as few as 120 variables are left unsolved after one hour using Gurobi 7.0.2. | 1 |  |
 |
| 2 | 30_70 | J. Walser | Geographic radar station allocation | 3 |  |
 |
| 3 | 8div | Sascha Kurz | Projective binary 8-divisible linear block codes A linear block code is called 8-divisible if the weights of its codewords are divisible by 8. It is called projective if there are no duplicate columns in the generator matrix. The possible lengths of 8-divisible linear block codes have been classified except for length n=59, where it is undecided whether such a linear code exists. The possible dimensions satisfy \\(10 \\le k \\le 20\\). Model 8div_n59_kXX contains the corresponding feasibility problem. Projective binary 8-divisible linear block codes occur as hole configurations of so-called partial solid spreads in finite geometry. Binary 4-divisible linear block codes have applications in physics. | 3 |  |
 |
| 4 | ab | MIPLIB submission pool | Imported from the MIPLIB2010 submissions. | 5 |  |
 |
| 5 | acc-tight | J. Walser | ACC basketball scheduling model | 3 |  |
 |
| 6 | aflow | T. Achterberg | Arborescence flow problem on a graph with 40 nodes and edge density 0.9 | 2 |  |
 |
| 7 | air | G. Astfalk | Airline crew scheduling set partitioning problem | 3 |  |
 |
| 8 | allcolor | Domenico Salvagnin | Prepack optimization model. | 2 |  |
 |
| 9 | amaze | Gleb Belov | These are the models from MiniZinc Challenges 2012-2016 (see www.minizinc.org), compiled for MIP WITH INDICATOR CONSTRAINTS using the develop branch of MiniZinc and CPLEX 12.7.1 on 30 April 2017. Thus, these models can only be handled by solvers accepting indicator constraints. For models compiled with big-M/domain decomposition only, see my previous submission to MIPLIB.To recompile, create a directory MODELS, a list lst12_16.txt of the models with full paths to mzn/dzn files of each model per line, and say$> ~/install/libmzn/tests/benchmarking/mzn-test.py -l ../lst12_16.txt -slvPrf MZN-CPLEX -debug 1 -addOption "-timeout 3 -D fIndConstr=true -D fMIPdomains=false" -useJoinedName "-writeModel MODELS_IND/%s.mps" Alternatively, you can compile individual model as follows: $> mzn-cplex -v -s -G linear -output-time ../challenge_2012_2016/mznc2016_probs/zephyrus/zephyrus.mzn ../challenge_2012_2016/mznc2016_p/zephyrus/14__8__6__3.dzn -a -timeout 3 -D fIndConstr=true -D fMIPdomains=false -writeModel MODELS_IND/challenge_2012_2016mznc2016_probszephyruszephyrusmzn-challenge_2012_2016mznc2016_probszephyrus14__8__6__3dzn.mps | 3 |  |
 |
| 10 | app | Emilie Danna | The archive contains 5 models coming from 3 applications.app1 is interesting because the continuous variables (w) drive the model.Some solvers have numerical problems on app2 models: some solutions found violate the constraints by a small amount.app2 and app3 models are easy to solve. But they don't solve fast enough for the time limit I have in mind so I'd like to propose them for inclusion in MIPLIB. | 5 |  |
 |
| 11 | assign1 | Robert Fourer | Imported from the MIPLIB2010 submissions. | 2 |  |
 |
| 12 | bab | Elmar Swarat | Vehicle routing with profit and an integrated crew scheduling like bab2 - bab5. Models differ in multi-commodity-flow formulation (path oder arc formulation) or time discretization and some are quite easy to solve while others (bab2, bab3 and bab6) are very difficult. | 5 |  |
 |
| 13 | bc | MIPLIB submission pool | Imported from the MIPLIB2010 submissions. | 1 |  |
 |
| 14 | beasley | F. Ortega, L. Wolsey | Fixed cost network flow problems | 3 |  |
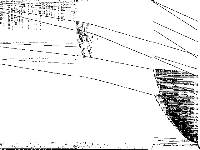
 |
| 15 | binpack | Simon Felix | Feasability-only 3D bin packing with additional constraints | 5 |  |
 |
| 16 | blp | M. Lübbecke | Railway line planning model. Solved using CPLEX 12.3 (12 threads) on an Intel Xeon X5650 @ 2.67GHz, 12MB cache, 24GB RAM in 4947.5 sec.\xa0Solved using Gurobi 4.6.1 (12 threads) in 1867.9 sec. | 4 |  |
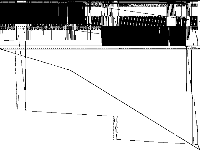
 |
| 17 | bmocbd | Sean MacDermant | BMOCBD2 | 2 |  |
 |
| 18 | bnatt | Tatsuya Akutsu | We are submitting ILP data for identification of a singletonattractor in a Boolean newtork, which is a well-known problemin computational systems biology.This problem is known to be NP-hard and we developed a methodto transform an model of the problem to an integer linearprogram (ILP).We used ILPs from artificially generated Boolean networks ofindegree 3.The size of the networks are: 350, 400, 500.Even for the case of 500, we could not find a solution within6 hours using CPLEX 11.2 on a PC with XEON 5470 3.33GHz CPU.(This ILP corresponds to the case of size=350.File format is (zipped) CPLEX LP format.)The details of the method appeared in:T. Akutsu, M. Hayashida and T. Tamura, Integer programming-basedmethods for attractor detection and control of Boolean networks,Proc. The combined 48th IEEE Conference on Decision and Controland 28th Chinese Control Conference (IEEE CDC/CCC 2009), 5610-5617, 2009. | 2 |  |
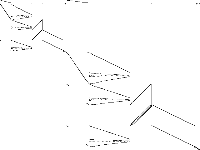
 |
| 19 | bppc | Manuel Iori | The models that we attach solve the "bar-relaxation", also known as the "Bin Packing Problem with Contiguity" or the "P||Cmax with contiguity". This is one of the most interesting relaxations for two dimensional cutting and packing problems. Its solution by means of an ILP software is the bottleneck of the primal decomposition methods that we attempted in the paper cited below. In detail, the files correspond to model (12)-(15) in the paper, applied to the models of the Classes 4, 6 and 8 by Martello and Vigo (Management Science, 1998). | 5 |  |
 |
| 20 | c1s1 | M. Vyve, Y. Pochet | Lot sizing model. | 3 |  |
 |
| 21 | chromaticindex | Pierre Le Bodic | Simple edge-coloring model on chains of Petersen-like subgraphs, designed to fool MIP solvers into producing very large Branch-and-Bound trees. | 5 |  |
 |
| 22 | cmflsp | Andrea Arias | Capacitated Multi-Family Lot-Sizing Problem | 5 |  |
 |
| 23 | control | Qie He | Optimal control of a discrete-time switched system model Numerically challenging. Different solvers report this model as solved to optimality, infeasible, or unbounded. | 3 |  |
 |
| 24 | core | A. Caprara, M. Fischetti, P. Toth | Set covering model coming from Italian railway models | 4 |  |
 |
| 25 | coursetimetabling | Matias Sørensen | Models comp01-21 of curriculum based course timetabling from the International Timetabling Competition 2007. These are time-assignment models (Stage I of the decomposed model), which are smaller than the full model, but still hard to solve. | 5 |  |
 |
| 26 | cryptanalysis | Gleb Belov | Linearized Constraint Programming models of the MiniZinc Challenges 2012-2016. I should be able to produce versions with indicator constraints supported by Gurobi and CPLEX, however don't know if you can use them and if there is a standard format. These MPS were produced by Gurobi 7.0.2 using the MiniZinc develop branch on eb536656062ca13325a96b5d0881742c7d0e3c38 | 2 |  |
 |
| 27 | csched | Tallys Yunes | Cumulative scheduling problem model | 3 |  |
 |
| 28 | cta | Jordi Castro | Set of MILP models of the CTA (Controlled Tabular Adjustment) problem, a method to protect statistical tabular data, belonging to the field of SDC (Statistical Disclosure Control). Raw data of models are real or pseudo-real, provided by several National Statistical Agencies. We generated the CTA problem for these data. | 5 |  |
 |
| 29 | cvs | Michael Bastubbe | Capacitated vertex separator problem on randomly generated hypergraph with 128 vertices and 89 hyperedges in at most 16 components each including at most 8 vertices. solved with default GCG/Soplex in about 2000 seconds. | 5 |  |
 |
| 30 | dano | Daniel Bienstock | Telecommunications applications | 5 |  |
 |
| 31 | diameterc | Gleb Belov | These are the models from MiniZinc Challenges 2012-2016 (see www.minizinc.org), compiled for MIP WITH INDICATOR CONSTRAINTS using the develop branch of MiniZinc and CPLEX 12.7.1 on 30 April 2017. Thus, these models can only be handled by solvers accepting indicator constraints. For models compiled with big-M/domain decomposition only, see my previous submission to MIPLIB.To recompile, create a directory MODELS, a list lst12_16.txt of the models with full paths to mzn/dzn files of each model per line, and say$> ~/install/libmzn/tests/benchmarking/mzn-test.py -l ../lst12_16.txt -slvPrf MZN-CPLEX -debug 1 -addOption "-timeout 3 -D fIndConstr=true -D fMIPdomains=false" -useJoinedName "-writeModel MODELS_IND/%s.mps" Alternatively, you can compile individual model as follows: $> mzn-cplex -v -s -G linear -output-time ../challenge_2012_2016/mznc2016_probs/zephyrus/zephyrus.mzn ../challenge_2012_2016/mznc2016_p/zephyrus/14__8__6__3.dzn -a -timeout 3 -D fIndConstr=true -D fMIPdomains=false -writeModel MODELS_IND/challenge_2012_2016mznc2016_probszephyruszephyrusmzn-challenge_2012_2016mznc2016_probszephyrus14__8__6__3dzn.mps | 2 |  |
 |
| 32 | drayage | F. Jordan Srour | The .rar file contains three folders: 1) R_mps with all of the models (165, organized into 5 groups R0_, R25_, R50_, R75_, and R100_*), 2) results_and_runtimes with datafiles on the runtime and results, and 3) doc with documentation on the models in the form of a pdf. | 1 | 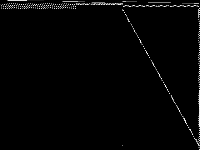 |
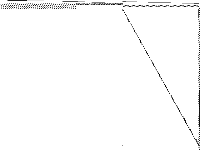 |
| 33 | dws | Philipp Leise | MILP for designing a decentralized water supply system for drinking water in skyscrapers. The nonlinear characteristics of pumps are integrated with the help of an aggregated convex combination. The models vary in the total number of floors and load scenarios for water demand. First stage variables represent the layout decisions, second stage variables represent the operational parameters, such as the continuous rotating speed of pumps or binary switching decisions. | 5 |  |
 |
| 34 | eil | J. Linderoth | Set partitioning problem approximation for capicated vehicle routing problem model from TSPLIB | 3 |  |
 |
| 35 | elitserienhandball | Gleb Belov | These are the models from MiniZinc Challenges 2012-2016 (see www.minizinc.org), compiled for MIP WITH INDICATOR CONSTRAINTS using the develop branch of MiniZinc and CPLEX 12.7.1 on 30 April 2017. Thus, these models can only be handled by solvers accepting indicator constraints. For models compiled with big-M/domain decomposition only, see my previous submission to MIPLIB.To recompile, create a directory MODELS, a list lst12_16.txt of the models with full paths to mzn/dzn files of each model per line, and say$> ~/install/libmzn/tests/benchmarking/mzn-test.py -l ../lst12_16.txt -slvPrf MZN-CPLEX -debug 1 -addOption "-timeout 3 -D fIndConstr=true -D fMIPdomains=false" -useJoinedName "-writeModel MODELS_IND/%s.mps" Alternatively, you can compile individual model as follows: $> mzn-cplex -v -s -G linear -output-time ../challenge_2012_2016/mznc2016_probs/zephyrus/zephyrus.mzn ../challenge_2012_2016/mznc2016_p/zephyrus/14__8__6__3.dzn -a -timeout 3 -D fIndConstr=true -D fMIPdomains=false -writeModel MODELS_IND/challenge_2012_2016mznc2016_probszephyruszephyrusmzn-challenge_2012_2016mznc2016_probszephyrus14__8__6__3dzn.mps | 4 | 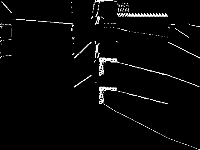 |
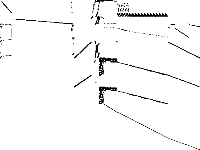 |
| 36 | enlight | A. Zymolka | Model to solve model of a combinatorial game ``EnLight'' Imported from the MIPLIB2010 submissions. | 5 |  |
 |
| 37 | evaprime | Yoshihiro Kanno | MILP approach to generate structures with negative thermal expansion coefficients | 2 |  |
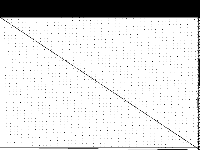
 |
| 38 | exp_and_fc | MIPLIB submission pool | Imported from the MIPLIB2010 submissions. | 5 |  |
 |
| 39 | f2gap | Salim Haddadi | Restrictions of well-known hard generalized assignment problem models (D10400,D20400,D40400,D15900,D30900,D60900,D201600,D401600,D801600) | 4 |  |
 |
| 40 | fastxgemm | Laurent Sorber | Naive multiplication of two N by N matrices requires N^3 scalar multiplications. For N=2, Strassen showed that it could be done in only R=7 < 8=N^3 multiplications. For N=3, it is known that 19 <= R <= 23, and for N=4 it is known that 34 <= R <= 49. This repository contains code that generates a mixed-integer linear program (MILP) formulation of the fast matrix multiplication problem for finding solutions with R < N^3 and proving that they are optimal. For a more detailed description, see the accompanying manuscript. | 5 |  |
 |
| 41 | fhnw-bin | Simon Felix | Scheduling/assignment for an industrial production pipeline | 3 | 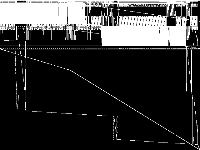 |
 |
| 42 | fhnw-sq | Simon Felix | Combinatorial toy fesability problem: Magic square. Models 1 & 2 are feasible, model 3 is unknown. | 2 |  |
 |
| 43 | fillomino | Gleb Belov | These are the models from MiniZinc Challenges 2012-2016 (see www.minizinc.org), compiled for MIP WITH INDICATOR CONSTRAINTS using the develop branch of MiniZinc and CPLEX 12.7.1 on 30 April 2017. Thus, these models can only be handled by solvers accepting indicator constraints. For models compiled with big-M/domain decomposition only, see my previous submission to MIPLIB.To recompile, create a directory MODELS, a list lst12_16.txt of the models with full paths to mzn/dzn files of each model per line, and say$> ~/install/libmzn/tests/benchmarking/mzn-test.py -l ../lst12_16.txt -slvPrf MZN-CPLEX -debug 1 -addOption "-timeout 3 -D fIndConstr=true -D fMIPdomains=false" -useJoinedName "-writeModel MODELS_IND/%s.mps" Alternatively, you can compile individual model as follows: $> mzn-cplex -v -s -G linear -output-time ../challenge_2012_2016/mznc2016_probs/zephyrus/zephyrus.mzn ../challenge_2012_2016/mznc2016_p/zephyrus/14__8__6__3.dzn -a -timeout 3 -D fIndConstr=true -D fMIPdomains=false -writeModel MODELS_IND/challenge_2012_2016mznc2016_probszephyruszephyrusmzn-challenge_2012_2016mznc2016_probszephyrus14__8__6__3dzn.mps | 1 |  |
 |
| 44 | fixed-cost-network-flow | MIPLIB submission pool | Imported from the MIPLIB2010 submissions. | 5 |  |
 |
| 45 | fjsp | Gleb Belov | These are the models from MiniZinc Challenges 2012-2016 (see www.minizinc.org), compiled for MIP WITH INDICATOR CONSTRAINTS using the develop branch of MiniZinc and CPLEX 12.7.1 on 30 April 2017. Thus, these models can only be handled by solvers accepting indicator constraints. For models compiled with big-M/domain decomposition only, see my previous submission to MIPLIB.To recompile, create a directory MODELS, a list lst12_16.txt of the models with full paths to mzn/dzn files of each model per line, and say$> ~/install/libmzn/tests/benchmarking/mzn-test.py -l ../lst12_16.txt -slvPrf MZN-CPLEX -debug 1 -addOption "-timeout 3 -D fIndConstr=true -D fMIPdomains=false" -useJoinedName "-writeModel MODELS_IND/%s.mps" Alternatively, you can compile individual model as follows: $> mzn-cplex -v -s -G linear -output-time ../challenge_2012_2016/mznc2016_probs/zephyrus/zephyrus.mzn ../challenge_2012_2016/mznc2016_p/zephyrus/14__8__6__3.dzn -a -timeout 3 -D fIndConstr=true -D fMIPdomains=false -writeModel MODELS_IND/challenge_2012_2016mznc2016_probszephyruszephyrusmzn-challenge_2012_2016mznc2016_probszephyrus14__8__6__3dzn.mps | 1 | 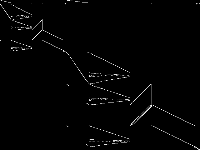 |
 |
| 46 | gasprod | Andrew Stamps | Production planning model of a second industrial gas system. Two model models included. | 5 |  |
 |
| 47 | generated | Simon Bowly | Randomly generated integer and binary programming models. These results are part of an early phase of work aimed at generating diverse and challenging MIP models for experimental testing. We have aimed to produce small integer and binary programming models which are reasonably difficult to solve and have varied structure, eliciting a range of behaviour in state of the art algorithms. | 5 |  |
 |
| 48 | genus | Stephan Beyer | Minimum Genus model, with symmetry breaking constraints, of g.31.8 (undirected) of the AT&T Graphs by Stephen C. North. | 5 |  |
 |
| 49 | ger50 | C. Raack | Multi-layer network design problem using a link-flow formulation over a path-flow formulation. | 3 |  |
 |
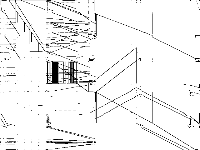
| 50 | gfd-schedule | Gleb Belov | These are the models from MiniZinc Challenges 2012-2016 (see www.minizinc.org), compiled for MIP WITH INDICATOR CONSTRAINTS using the develop branch of MiniZinc and CPLEX 12.7.1 on 30 April 2017. Thus, these models can only be handled by solvers accepting indicator constraints. For models compiled with big-M/domain decomposition only, see my previous submission to MIPLIB.To recompile, create a directory MODELS, a list lst12_16.txt of the models with full paths to mzn/dzn files of each model per line, and say$> ~/install/libmzn/tests/benchmarking/mzn-test.py -l ../lst12_16.txt -slvPrf MZN-CPLEX -debug 1 -addOption "-timeout 3 -D fIndConstr=true -D fMIPdomains=false" -useJoinedName "-writeModel MODELS_IND/%s.mps" Alternatively, you can compile individual model as follows: $> mzn-cplex -v -s -G linear -output-time ../challenge_2012_2016/mznc2016_probs/zephyrus/zephyrus.mzn ../challenge_2012_2016/mznc2016_p/zephyrus/14__8__6__3.dzn -a -timeout 3 -D fIndConstr=true -D fMIPdomains=false -writeModel MODELS_IND/challenge_2012_2016mznc2016_probszephyruszephyrusmzn-challenge_2012_2016mznc2016_probszephyrus14__8__6__3dzn.mps | 3 | 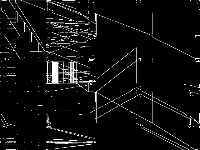 |
 |
| 51 | ghoulomb | Gleb Belov | These are the models from MiniZinc Challenges 2012-2016 (see www.minizinc.org), compiled for MIP WITH INDICATOR CONSTRAINTS using the develop branch of MiniZinc and CPLEX 12.7.1 on 30 April 2017. Thus, these models can only be handled by solvers accepting indicator constraints. For models compiled with big-M/domain decomposition only, see my previous submission to MIPLIB.To recompile, create a directory MODELS, a list lst12_16.txt of the models with full paths to mzn/dzn files of each model per line, and say$> ~/install/libmzn/tests/benchmarking/mzn-test.py -l ../lst12_16.txt -slvPrf MZN-CPLEX -debug 1 -addOption "-timeout 3 -D fIndConstr=true -D fMIPdomains=false" -useJoinedName "-writeModel MODELS_IND/%s.mps" Alternatively, you can compile individual model as follows: $> mzn-cplex -v -s -G linear -output-time ../challenge_2012_2016/mznc2016_probs/zephyrus/zephyrus.mzn ../challenge_2012_2016/mznc2016_p/zephyrus/14__8__6__3.dzn -a -timeout 3 -D fIndConstr=true -D fMIPdomains=false -writeModel MODELS_IND/challenge_2012_2016mznc2016_probszephyruszephyrusmzn-challenge_2012_2016mznc2016_probszephyrus14__8__6__3dzn.mps | 1 | 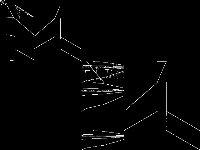 |
 |
| 52 | gmu | Nora Konnyu | Timber harvest scheduling model These are harvest scheduling models of hypothetical forest planning problems where net timber revenues are maximized over a planning horizon subject to four sets of constraints: 1. Each management unit can be harvested only once over the planning horizon, 2. Volume harvested in one planning period should not be less or more than some portion of that in the preceding period, 3. Area-weighted average age of the forest by the end of the plan should notbe less than a certain target age. 4. Clearcut size in any planning period has to be below a specific limit. Decision variable are management units and generalized management units (group of management units with a combined area not exceeding the limit on clearcut size) and can be either fully harvested or left untouched in any planning period, therefore there is a binary restriction on the decision variables. | 5 |  |
 |
| 53 | graphdraw | Cézar Augusto Nascimento e Silva | In the Graph Drawing problem a set of symbols must be placed in a plane and their connections routed. The objective is to produce aesthetically pleasant, easy to read diagrams. As a primary concern one usually tries to minimize edges crossing, edges' length, waste of space and number of bents in the connections. When formulated with these constraints the problem becomes NP-Hard . In practice many additional complicating requirements can be included, such as non-uniform sizes for symbols. Thus, some heuristics such as the generalized force-direct method and Simulated Annealing have been proposed to tackle this problem. uses a grid structure to approach the Entity-Relationship (ER) drawing problem, emphasizing the differences between ER drawing and the more classical circuit drawing problems. presented different ways of producing graph layouts (e.g.: tree, orthogonal, visibility representations, hierarchic, among others) for general graphs with applications on different subjects. The ability to automatically produce high quality layouts is very important in many applications, one of these is Software Engineering: the availability of easy to understand ER diagrams, for model, can improve the time needed for developers to master database models and increase their productivity. Our solution approach involves two phases: (\\(i\\)) firstly the optimal placement of entities is solved, i.e.: entities are positioned so as to minimize the distances between connected entities; and (\\(ii\\)) secondly, edges are routed minimizing bends and avoiding the inclusion of connectors too close. We present the model for the first phase of our problem. | 5 |  |
 |
| 54 | graphs | Michael Bastubbe | Packing Cuts in Undirected Graphs. Models are described in 4.1. | 5 |  |
 |
| 55 | hgms | Jesus Rodriguez | Maintenance scheduling of generators in hydropower systems | 3 |  |
 |
| 56 | huefner | Falk Hueffner | The NP-hard Balanced Subgraph problem (variant of MaxCut) encoded as ILPs. Real-world models from two applications from bioinformatics, finding monotone subsystems in gene regulatory networks (http://dx.doi.org/10.1007/s10878-009-9212-2) and finding optimal layouts of tanglegrams (http://dx.doi.org/10.1007/978-3-642-11269-0). | 3 |  |
 |
| 57 | hypothyroid | Gleb Belov | Linearized Constraint Programming models of the MiniZinc Challenges 2012-2016. I should be able to produce versions with indicator constraints supported by Gurobi and CPLEX, however don't know if you can use them and if there is a standard format. These MPS were produced by Gurobi 7.0.2 using the MiniZinc develop branch on eb536656062ca13325a96b5d0881742c7d0e3c38 | 1 |  |
 |
| 58 | iis | Marc Pfetsch | 23 "middlehard" Set-Covering Models for MIPLIB: they have a small number of variables compared to the number of constraints and CPLEX 12.1 needs about one hour to solve them.For more information, have a look into the readme file which explains how the models can be created. | 2 |  |
 |
| 59 | independentset | Toni Sorrell | These models are based on Neil Sloane's Challenge problems: Independent Sets in Graphs. | 4 |  |
 |
| 60 | ivu | S. Weider | Set partitioning model resulting from a column generation algorithm used for duty scheduling in public transportation. Solved in June 2014 using CPLEX 12.6 with 48 threads in about 25 days. | 2 | 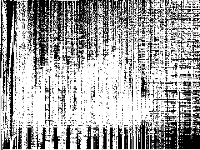 |
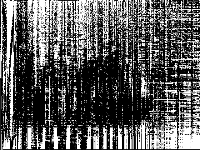 |
| 61 | k1mushroom | Gleb Belov | Linearized Constraint Programming models of the MiniZinc Challenges 2012-2016. I should be able to produce versions with indicator constraints supported by Gurobi and CPLEX, however don't know if you can use them and if there is a standard format. These MPS were produced by Gurobi 7.0.2 using the MiniZinc develop branch on eb536656062ca13325a96b5d0881742c7d0e3c38 | 2 | 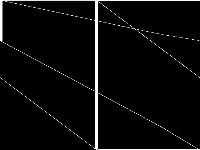 |
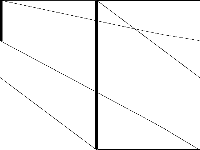 |
| 62 | l2p | Gleb Belov | These are the models from MiniZinc Challenges 2012-2016 (see www.minizinc.org), compiled for MIP WITH INDICATOR CONSTRAINTS using the develop branch of MiniZinc and CPLEX 12.7.1 on 30 April 2017. Thus, these models can only be handled by solvers accepting indicator constraints. For models compiled with big-M/domain decomposition only, see my previous submission to MIPLIB.To recompile, create a directory MODELS, a list lst12_16.txt of the models with full paths to mzn/dzn files of each model per line, and say$> ~/install/libmzn/tests/benchmarking/mzn-test.py -l ../lst12_16.txt -slvPrf MZN-CPLEX -debug 1 -addOption "-timeout 3 -D fIndConstr=true -D fMIPdomains=false" -useJoinedName "-writeModel MODELS_IND/%s.mps" Alternatively, you can compile individual model as follows: $> mzn-cplex -v -s -G linear -output-time ../challenge_2012_2016/mznc2016_probs/zephyrus/zephyrus.mzn ../challenge_2012_2016/mznc2016_p/zephyrus/14__8__6__3.dzn -a -timeout 3 -D fIndConstr=true -D fMIPdomains=false -writeModel MODELS_IND/challenge_2012_2016mznc2016_probszephyruszephyrusmzn-challenge_2012_2016mznc2016_probszephyrus14__8__6__3dzn.mps | 3 |  |
 |
| 63 | lectsched | Harald Schilly | University lecture scheduling model | 5 |  |
 |
| 64 | map | Kiyan Ahmadizadeh | Land parcel selection problems motivated by Red-Cockaded Woodpecker conservation problem | 1 |  |
 |
| 65 | mapping | Gleb Belov | These are the models from MiniZinc Challenges 2012-2016 (see www.minizinc.org), compiled for MIP WITH INDICATOR CONSTRAINTS using the develop branch of MiniZinc and CPLEX 12.7.1 on 30 April 2017. Thus, these models can only be handled by solvers accepting indicator constraints. For models compiled with big-M/domain decomposition only, see my previous submission to MIPLIB.To recompile, create a directory MODELS, a list lst12_16.txt of the models with full paths to mzn/dzn files of each model per line, and say$> ~/install/libmzn/tests/benchmarking/mzn-test.py -l ../lst12_16.txt -slvPrf MZN-CPLEX -debug 1 -addOption "-timeout 3 -D fIndConstr=true -D fMIPdomains=false" -useJoinedName "-writeModel MODELS_IND/%s.mps" Alternatively, you can compile individual model as follows: $> mzn-cplex -v -s -G linear -output-time ../challenge_2012_2016/mznc2016_probs/zephyrus/zephyrus.mzn ../challenge_2012_2016/mznc2016_p/zephyrus/14__8__6__3.dzn -a -timeout 3 -D fIndConstr=true -D fMIPdomains=false -writeModel MODELS_IND/challenge_2012_2016mznc2016_probszephyruszephyrusmzn-challenge_2012_2016mznc2016_probszephyrus14__8__6__3dzn.mps | 1 |  |
 |
| 66 | mario | Gleb Belov | These are the models from MiniZinc Challenges 2012-2016 (see www.minizinc.org), compiled for MIP WITH INDICATOR CONSTRAINTS using the develop branch of MiniZinc and CPLEX 12.7.1 on 30 April 2017. Thus, these models can only be handled by solvers accepting indicator constraints. For models compiled with big-M/domain decomposition only, see my previous submission to MIPLIB.To recompile, create a directory MODELS, a list lst12_16.txt of the models with full paths to mzn/dzn files of each model per line, and say$> ~/install/libmzn/tests/benchmarking/mzn-test.py -l ../lst12_16.txt -slvPrf MZN-CPLEX -debug 1 -addOption "-timeout 3 -D fIndConstr=true -D fMIPdomains=false" -useJoinedName "-writeModel MODELS_IND/%s.mps" Alternatively, you can compile individual model as follows: $> mzn-cplex -v -s -G linear -output-time ../challenge_2012_2016/mznc2016_probs/zephyrus/zephyrus.mzn ../challenge_2012_2016/mznc2016_p/zephyrus/14__8__6__3.dzn -a -timeout 3 -D fIndConstr=true -D fMIPdomains=false -writeModel MODELS_IND/challenge_2012_2016mznc2016_probszephyruszephyrusmzn-challenge_2012_2016mznc2016_probszephyrus14__8__6__3dzn.mps | 1 |  |
 |
| 67 | maritime | Dimitri Papageorgiou | Maritime Inventory Routing Problems: Jiang-Grossmann Models. These models are available at https://mirplib.scl.gatech.edu/models, along with a host of additional information such as the underlying data used to generate the model, best known upper and lower bounds, and more. They involve a single product maritime inventory routing problem and explore the use of continuous and discrete time models. A continuous-time model based on time slots for single docks is used for some models. A model based on event points to handle parallel docks is used in others. A discrete time model based on a single commodity fixed-charge network flow problem (FCNF) is used for other models. All the models are solved for multiple randomly generated models of different problems to compare their computational efficiency. | 5 |  |
 |
| 68 | markshare | G. Cornuéjols, M. Dawande | Market sharing problem | 4 |  |
 |
| 69 | maxfeassub | Marc Pfetsch | Set covering problems arising from a Benders algorithm for finding maximum feasible subsystems. More details on the generation is given in the README file in the tarball. | 1 |  |
 |
| 70 | mc | F. Ortega, L. Wolsey | Fixed cost network flow problems | 1 |  |
 |
| 71 | mik_250 | MIPLIB submission pool | Imported from the MIPLIB2010 submissions. | 1 |  |
 |
| 72 | milo | Tamas Terlaky | The models come from structural design optimization where the objective is to minimize the total weight of 2 and 3 dimensional cantilevers. The 2D examples are simpler, and GuRobi can solve the 40_1 and 58_1 models, while struggles with 75_1. The 3D examples are more challenging. The x_0 and x_1 models are two different modeling of the same identical problems, so their optimal value is the same. The 1_x and 2_x problems are solved by GuRoBi, the 3_x and 4_x are not solved in reasonable time. | 5 |  |
 |
| 73 | mine | Andreas Bley | Multi-period mine production scheduling model | 2 |  |
 |
| 74 | misc | MIPLIB submission pool | Imported from the MIPLIB2010 submissions. | 3 |  |
 |
| 75 | mod | MIPLIB submission pool | Imported from the MIPLIB2010 submissions. | 3 |  |
 |
| 76 | momentum | T. Koch | Snapshot based UMTS planning problem, having a very wide dynamic range in the matrix coefficients and tending to be numerically unstable. Solved with Gurobi 4.5.1 on a 12-core Linux system in 3590.41 sec. | 3 |  |
 |
| 77 | mrcpspj | Gleb Belov | These are the models from MiniZinc Challenges 2012-2016 (see www.minizinc.org), compiled for MIP WITH INDICATOR CONSTRAINTS using the develop branch of MiniZinc and CPLEX 12.7.1 on 30 April 2017. Thus, these models can only be handled by solvers accepting indicator constraints. For models compiled with big-M/domain decomposition only, see my previous submission to MIPLIB.To recompile, create a directory MODELS, a list lst12_16.txt of the models with full paths to mzn/dzn files of each model per line, and say$> ~/install/libmzn/tests/benchmarking/mzn-test.py -l ../lst12_16.txt -slvPrf MZN-CPLEX -debug 1 -addOption "-timeout 3 -D fIndConstr=true -D fMIPdomains=false" -useJoinedName "-writeModel MODELS_IND/%s.mps" Alternatively, you can compile individual model as follows: $> mzn-cplex -v -s -G linear -output-time ../challenge_2012_2016/mznc2016_probs/zephyrus/zephyrus.mzn ../challenge_2012_2016/mznc2016_p/zephyrus/14__8__6__3.dzn -a -timeout 3 -D fIndConstr=true -D fMIPdomains=false -writeModel MODELS_IND/challenge_2012_2016mznc2016_probszephyruszephyrusmzn-challenge_2012_2016mznc2016_probszephyrus14__8__6__3dzn.mps | 3 |  |
 |
| 78 | mspsp | Gleb Belov | These are the models from MiniZinc Challenges 2012-2016 (see www.minizinc.org), compiled for MIP WITH INDICATOR CONSTRAINTS using the develop branch of MiniZinc and CPLEX 12.7.1 on 30 April 2017. Thus, these models can only be handled by solvers accepting indicator constraints. For models compiled with big-M/domain decomposition only, see my previous submission to MIPLIB.To recompile, create a directory MODELS, a list lst12_16.txt of the models with full paths to mzn/dzn files of each model per line, and say$> ~/install/libmzn/tests/benchmarking/mzn-test.py -l ../lst12_16.txt -slvPrf MZN-CPLEX -debug 1 -addOption "-timeout 3 -D fIndConstr=true -D fMIPdomains=false" -useJoinedName "-writeModel MODELS_IND/%s.mps" Alternatively, you can compile individual model as follows: $> mzn-cplex -v -s -G linear -output-time ../challenge_2012_2016/mznc2016_probs/zephyrus/zephyrus.mzn ../challenge_2012_2016/mznc2016_p/zephyrus/14__8__6__3.dzn -a -timeout 3 -D fIndConstr=true -D fMIPdomains=false -writeModel MODELS_IND/challenge_2012_2016mznc2016_probszephyruszephyrusmzn-challenge_2012_2016mznc2016_probszephyrus14__8__6__3dzn.mps | 2 |  |
 |
| 79 | n37 | J. Aronson | Fixed charge transportation problem | 1 |  |
 |
| 80 | neos-pseudoapplication-1 | NEOS Server Submission | Imported from the MIPLIB2010 submissions. | 1 |  |
 |
| 81 | neos-pseudoapplication-10 | NEOS Server Submission | Collection of anonymous submissions to the NEOS Server for Optimization | 3 |  |
 |
| 82 | neos-pseudoapplication-100 | NEOS Server Submission | Model coming from the NEOS Server with unknown application | 3 |  |
 |
| 83 | neos-pseudoapplication-101 | NEOS Server Submission | Model coming from the NEOS Server with unknown application. Infeasibility claimed by CPLEX 12.6 and CPLEX 12.6.1 with extreme numerical caution emphasi after 4 and 2 hours computation, respectively. | 2 | 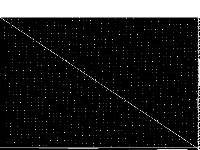 |
 |
| 84 | neos-pseudoapplication-102 | Hans Mittelmann | Seem to be VRP output from 2-hour runs of Gurobi on 12 threads is included | 5 |  |
 |
| 85 | neos-pseudoapplication-103 | Hans Mittelmann | Collection of anonymous submissions to the NEOS Server for Optimization | 2 |  |
 |
| 86 | neos-pseudoapplication-104 | Jeff Linderoth | (None provided) | 5 |  |
 |
| 87 | neos-pseudoapplication-105 | Jeff Linderoth | (None provided) | 5 |  |
 |
| 88 | neos-pseudoapplication-106 | Hans Mittelmann | Collection of anonymous submissions to the NEOS Server for Optimization | 4 |  |
 |
| 89 | neos-pseudoapplication-107 | Jeff Linderoth | (None provided) | 1 | 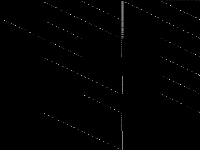 |
 |
| 90 | neos-pseudoapplication-108 | NEOS Server Submission | Model coming from the NEOS Server with unknown application | 1 |  |
 |
| 91 | neos-pseudoapplication-109 | Jeff Linderoth | (None provided) | 1 |  |
 |
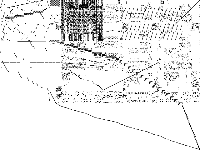
| 92 | neos-pseudoapplication-11 | NEOS Server Submission | Imported from the MIPLIB2010 submissions. | 3 |  |
 |
| 93 | neos-pseudoapplication-110 | Jeff Linderoth | (None provided) | 5 |  |
 |
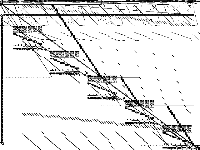
| 94 | neos-pseudoapplication-12 | NEOS Server Submission | Imported from the MIPLIB2010 submissions. | 5 |  |
 |
| 95 | neos-pseudoapplication-13 | NEOS Server Submission | Model coming from the NEOS Server with unknown application | 5 |  |
 |
| 96 | neos-pseudoapplication-14 | Jeff Linderoth | (None provided) | 2 | 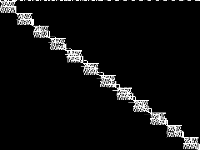 |
 |
| 97 | neos-pseudoapplication-15 | NEOS Server Submission | Imported from the MIPLIB2010 submissions. | 5 | 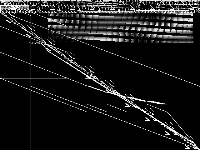 |
 |
| 98 | neos-pseudoapplication-17 | Jeff Linderoth | (None provided) | 5 |  |
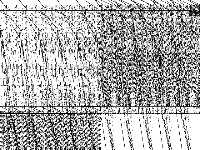
 |
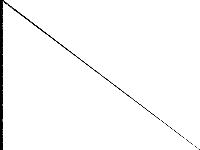
| 99 | neos-pseudoapplication-19 | Hans Mittelmann | similar to model ns5223573 submitted in January Solved with ParaSCIP in 525353 seconds with 71 solvers(72 cores). | 3 |  |
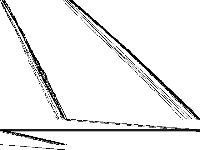
 |
| 100 | neos-pseudoapplication-2 | NEOS Server Submission | Imported from the MIPLIB2010 submissions. | 1 |  |
 |
| 101 | neos-pseudoapplication-20 | Jeff Linderoth | (None provided) | 1 |  |
 |
| 102 | neos-pseudoapplication-21 | NEOS Server Submission | Imported from the MIPLIB2010 submissions. | 1 |  |
 |
| 103 | neos-pseudoapplication-22 | Jeff Linderoth | (None provided) | 2 |  |
 |
| 104 | neos-pseudoapplication-23 | NEOS Server Submission | Imported from the MIPLIB2010 submissions. | 2 |  |
 |
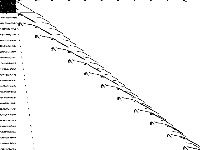
| 105 | neos-pseudoapplication-24 | Jeff Linderoth | (None provided) | 4 |  |
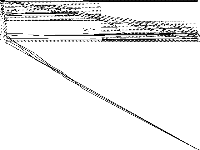 |
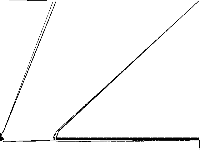
| 106 | neos-pseudoapplication-25 | NEOS Server Submission | Model coming from the NEOS Server with unknown application | 5 |  |
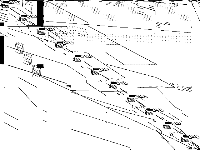 |
| 107 | neos-pseudoapplication-26 | NEOS Server Submission | Imported from the MIPLIB2010 submissions. | 4 |  |
 |
| 108 | neos-pseudoapplication-27 | NEOS Server Submission | Imported from the MIPLIB2010 submissions. | 1 |  |
 |
| 109 | neos-pseudoapplication-29 | Hans Mittelmann | Collection of anonymous submissions to the NEOS Server for Optimization | 3 |  |
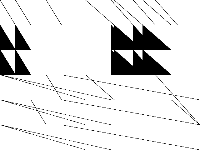 |
| 110 | neos-pseudoapplication-3 | NEOS Server Submission | Imported from the MIPLIB2010 submissions. | 5 |  |
 |
| 111 | neos-pseudoapplication-30 | Jeff Linderoth | (None provided) | 5 |  |
 |
| 112 | neos-pseudoapplication-31 | Jeff Linderoth | (None provided) | 5 |  |
 |
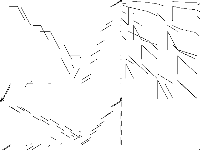
| 113 | neos-pseudoapplication-32 | NEOS Server Submission | Imported from the MIPLIB2010 submissions. | 4 |  |
 |
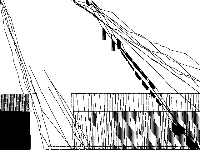
| 114 | neos-pseudoapplication-34 | NEOS Server Submission | Model coming from the NEOS Server with unknown application | 5 |  |
 |
| 115 | neos-pseudoapplication-35 | Jeff Linderoth | (None provided) | 3 |  |
 |
| 116 | neos-pseudoapplication-36 | Jeff Linderoth | (None provided) | 2 |  |
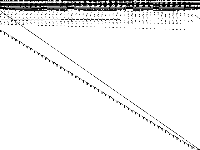 |
| 117 | neos-pseudoapplication-37 | Jeff Linderoth | (None provided) | 5 |  |
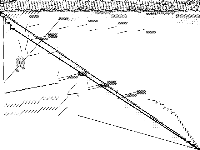 |
| 118 | neos-pseudoapplication-38 | Jeff Linderoth | (None provided) | 5 |  |
 |
| 119 | neos-pseudoapplication-4 | Jeff Linderoth | (None provided) | 2 |  |
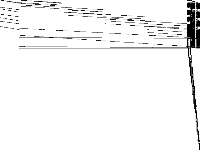 |
| 120 | neos-pseudoapplication-40 | Jeff Linderoth | (None provided) | 1 |  |
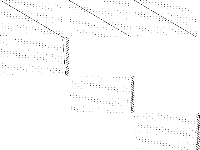 |
| 121 | neos-pseudoapplication-41 | Jeff Linderoth | (None provided) | 2 | 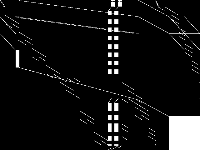 |
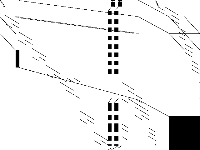 |
| 122 | neos-pseudoapplication-42 | Jeff Linderoth | (None provided) | 2 |  |
 |
| 123 | neos-pseudoapplication-43 | Jeff Linderoth | (None provided) | 4 |  |
 |
| 124 | neos-pseudoapplication-44 | Jeff Linderoth | (None provided) | 5 |  |
 |
| 125 | neos-pseudoapplication-45 | Jeff Linderoth | (None provided) | 4 |  |
 |
| 126 | neos-pseudoapplication-46 | NEOS Server Submission | Imported from the MIPLIB2010 submissions. | 5 |  |
 |
| 127 | neos-pseudoapplication-47 | NEOS Server Submission | Imported from the MIPLIB2010 submissions. | 4 |  |
 |
| 128 | neos-pseudoapplication-48 | NEOS Server Submission | Imported from the MIPLIB2010 submissions. | 5 |  |
 |
| 129 | neos-pseudoapplication-49 | NEOS Server Submission | Imported from the MIPLIB2010 submissions. | 3 |  |
 |
| 130 | neos-pseudoapplication-5 | NEOS Server Submission | Imported from the MIPLIB2010 submissions. | 5 |  |
 |
| 131 | neos-pseudoapplication-50 | NEOS Server Submission | Model coming from the NEOS Server with unknown application | 3 |  |
 |
| 132 | neos-pseudoapplication-51 | NEOS Server Submission | Model coming from the NEOS Server with unknown application | 5 |  |
 |
| 133 | neos-pseudoapplication-52 | Jeff Linderoth | (None provided) | 4 |  |
 |
| 134 | neos-pseudoapplication-53 | Hans Mittelmann | NEOS submission with known submitter | 1 |  |
 |
| 135 | neos-pseudoapplication-54 | Jeff Linderoth | (None provided) | 1 |  |
 |
| 136 | neos-pseudoapplication-56 | Jeff Linderoth | (None provided) | 5 |  |
 |
| 137 | neos-pseudoapplication-57 | Jeff Linderoth | (None provided) | 5 |  |
 |
| 138 | neos-pseudoapplication-58 | Jeff Linderoth | (None provided) | 4 |  |
 |
| 139 | neos-pseudoapplication-59 | Jeff Linderoth | (None provided) | 5 |  |
 |
| 140 | neos-pseudoapplication-6 | Jeff Linderoth | (None provided) | 5 |  |
 |
| 141 | neos-pseudoapplication-60 | NEOS Server Submission | Model coming from the NEOS Server with unknown application | 2 |  |
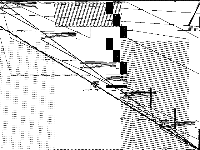
 |
| 142 | neos-pseudoapplication-61 | NEOS Server Submission | Imported from the MIPLIB2010 submissions. | 4 |  |
 |
| 143 | neos-pseudoapplication-62 | Hans Mittelmann | Collection of anonymous submissions to the NEOS Server for Optimization | 5 |  |
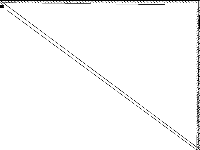
 |
| 144 | neos-pseudoapplication-63 | Jeff Linderoth | (None provided) | 1 | 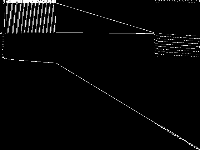 |
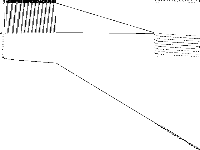 |
| 145 | neos-pseudoapplication-64 | Hans Mittelmann | Collection of anonymous submissions to the NEOS Server for Optimization | 2 |  |
 |
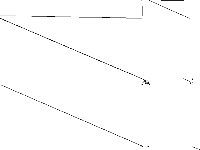
| 146 | neos-pseudoapplication-65 | NEOS Server Submission | Imported from the MIPLIB2010 submissions. | 1 | 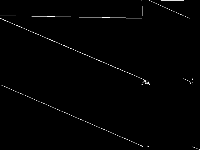 |
 |
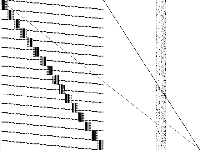
| 147 | neos-pseudoapplication-66 | NEOS Server Submission | Imported from the MIPLIB2010 submissions. | 2 | 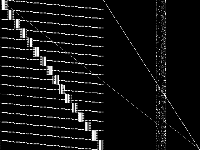 |
 |
| 148 | neos-pseudoapplication-67 | Jeff Linderoth | (None provided) | 4 |  |
 |
| 149 | neos-pseudoapplication-69 | Jeff Linderoth | (None provided) | 2 |  |
 |
| 150 | neos-pseudoapplication-7 | Jeff Linderoth | (None provided) | 5 |  |
 |
| 151 | neos-pseudoapplication-70 | NEOS Server Submission | Imported from the MIPLIB2010 submissions. | 2 |  |
 |
| 152 | neos-pseudoapplication-71 | Jeff Linderoth | (None provided) | 3 |  |
 |
| 153 | neos-pseudoapplication-72 | Jeff Linderoth | (None provided) | 3 |  |
 |
| 154 | neos-pseudoapplication-73 | NEOS Server Submission | Imported from the MIPLIB2010 submissions. | 1 |  |
 |
| 155 | neos-pseudoapplication-74 | Jeff Linderoth | (None provided) | 1 |  |
 |
| 156 | neos-pseudoapplication-75 | NEOS Server Submission | Imported from the MIPLIB2010 submissions. | 3 |  |
 |
| 157 | neos-pseudoapplication-76 | Jeff Linderoth | (None provided) | 5 | 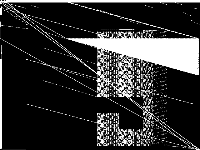 |
 |
| 158 | neos-pseudoapplication-77 | Jeff Linderoth | (None provided) | 5 | 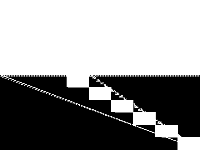 |
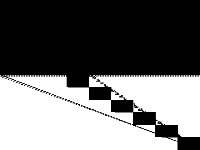 |
| 159 | neos-pseudoapplication-78 | Jeff Linderoth | (None provided) | 3 | 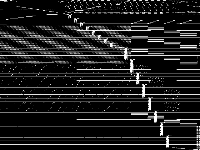 |
 |
| 160 | neos-pseudoapplication-79 | Jeff Linderoth | (None provided) | 2 |  |
 |
| 161 | neos-pseudoapplication-8 | NEOS Server Submission | Model coming from the NEOS Server with unknown application | 4 |  |
 |
| 162 | neos-pseudoapplication-80 | NEOS Server Submission | Model coming from the NEOS Server with unknown application | 1 |  |
 |
| 163 | neos-pseudoapplication-81 | Hans Mittelmann | Collection of anonymous submissions to the NEOS Server for Optimization | 3 |  |
 |
| 164 | neos-pseudoapplication-82 | NEOS Server Submission | Imported from the MIPLIB2010 submissions. | 5 |  |
 |
| 165 | neos-pseudoapplication-83 | NEOS Server Submission | Imported from the MIPLIB2010 submissions. | 3 |  |
 |
| 166 | neos-pseudoapplication-84 | Jeff Linderoth | (None provided) | 1 |  |
 |
| 167 | neos-pseudoapplication-85 | Jeff Linderoth | (None provided) | 5 |  |
 |
| 168 | neos-pseudoapplication-86 | Jeff Linderoth | (None provided) | 2 |  |
 |
| 169 | neos-pseudoapplication-87 | NEOS Server Submission | Imported from the MIPLIB2010 submissions. | 5 |  |
 |
| 170 | neos-pseudoapplication-88 | NEOS Server Submission | Imported from the MIPLIB2010 submissions. | 4 |  |
 |
| 171 | neos-pseudoapplication-89 | NEOS Server Submission | Model coming from the NEOS Server with unknown application | 2 |  |
 |
| 172 | neos-pseudoapplication-9 | NEOS Server Submission | Model coming from the NEOS Server with unknown application. | 5 |  |
 |
| 173 | neos-pseudoapplication-90 | NEOS Server Submission | Model coming from the NEOS Server with unknown application | 4 |  |
 |
| 174 | neos-pseudoapplication-91 | Jeff Linderoth | (None provided) | 5 |  |
 |
| 175 | neos-pseudoapplication-92 | NEOS Server Submission | Imported from the MIPLIB2010 submissions. | 2 |  |
 |
| 176 | neos-pseudoapplication-93 | NEOS Server Submission | Model coming from the NEOS Server with unknown application | 5 |  |
 |
| 177 | neos-pseudoapplication-94 | NEOS Server Submission | Imported from the MIPLIB2010 submissions. | 5 |  |
 |
| 178 | neos-pseudoapplication-95 | NEOS Server Submission | Imported from the MIPLIB2010 submissions. | 2 |  |
 |
| 179 | neos-pseudoapplication-96 | NEOS Server Submission | Imported from the MIPLIB2010 submissions. | 2 |  |
 |
| 180 | neos-pseudoapplication-97 | Jeff Linderoth | (None provided) | 1 |  |
 |
| 181 | neos-pseudoapplication-98 | NEOS Server Submission | Imported from the MIPLIB2010 submissions. | 4 |  |
 |
| 182 | neos-pseudoapplication-99 | NEOS Server Submission | Imported from the MIPLIB2010 submissions. | 1 |  |
 |
| 183 | network_design | MIPLIB submission pool | Imported from the MIPLIB2010 submissions. | 5 |  |
 |
| 184 | nj | Jonathan Eckstein | Electoral district design with various levels of symmetry breaking constraints. | 3 | 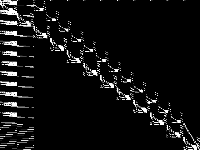 |
 |
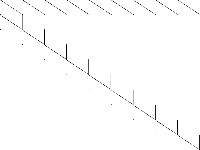
| 185 | noip | Christopher Hojny | integer programming formulation that verifies that no integer programming formulation of a given 0/1-point set exists | 1 | 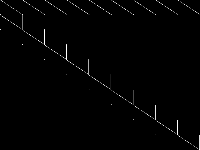 |
 |
| 186 | nseq | R. Meirich | Static line planning models on the Dutch IC network | 4 | 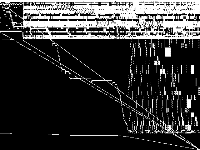 |
 |
| 187 | nursescheduling | Haroldo Gambini Santos | Nurse Scheduling Problems from the First International Nurse Rostering Competition - INRC 2010 | 5 |  |
 |
| 188 | nus-prxy | MIPLIB submission pool | Imported from the MIPLIB2010 submissions. | 3 |  |
 |
| 189 | nxy-z | A. Atamtürk | Capacitated network design problem | 5 |  |
 |
| 190 | oocsp-racks | Gleb Belov | These are the models from MiniZinc Challenges 2012-2016 (see www.minizinc.org), compiled for MIP WITH INDICATOR CONSTRAINTS using the develop branch of MiniZinc and CPLEX 12.7.1 on 30 April 2017. Thus, these models can only be handled by solvers accepting indicator constraints. For models compiled with big-M/domain decomposition only, see my previous submission to MIPLIB.To recompile, create a directory MODELS, a list lst12_16.txt of the models with full paths to mzn/dzn files of each model per line, and say$> ~/install/libmzn/tests/benchmarking/mzn-test.py -l ../lst12_16.txt -slvPrf MZN-CPLEX -debug 1 -addOption "-timeout 3 -D fIndConstr=true -D fMIPdomains=false" -useJoinedName "-writeModel MODELS_IND/%s.mps" Alternatively, you can compile individual model as follows: $> mzn-cplex -v -s -G linear -output-time ../challenge_2012_2016/mznc2016_probs/zephyrus/zephyrus.mzn ../challenge_2012_2016/mznc2016_p/zephyrus/14__8__6__3.dzn -a -timeout 3 -D fIndConstr=true -D fMIPdomains=false -writeModel MODELS_IND/challenge_2012_2016mznc2016_probszephyruszephyrusmzn-challenge_2012_2016mznc2016_probszephyrus14__8__6__3dzn.mps | 2 |  |
 |
| 191 | opm2 | Daniel Espinoza | Problems coming from precedence constrained knapsacks arising in mining applications. These are one-period problems with integer data but large root LP GAP | 5 |  |
 |
| 192 | pb- | Gleb Belov | These are the models from MiniZinc Challenges 2012-2016 (see www.minizinc.org), compiled for MIP WITH INDICATOR CONSTRAINTS using the develop branch of MiniZinc and CPLEX 12.7.1 on 30 April 2017. Thus, these models can only be handled by solvers accepting indicator constraints. For models compiled with big-M/domain decomposition only, see my previous submission to MIPLIB.To recompile, create a directory MODELS, a list lst12_16.txt of the models with full paths to mzn/dzn files of each model per line, and say$> ~/install/libmzn/tests/benchmarking/mzn-test.py -l ../lst12_16.txt -slvPrf MZN-CPLEX -debug 1 -addOption "-timeout 3 -D fIndConstr=true -D fMIPdomains=false" -useJoinedName "-writeModel MODELS_IND/%s.mps" Alternatively, you can compile individual model as follows: $> mzn-cplex -v -s -G linear -output-time ../challenge_2012_2016/mznc2016_probs/zephyrus/zephyrus.mzn ../challenge_2012_2016/mznc2016_p/zephyrus/14__8__6__3.dzn -a -timeout 3 -D fIndConstr=true -D fMIPdomains=false -writeModel MODELS_IND/challenge_2012_2016mznc2016_probszephyruszephyrusmzn-challenge_2012_2016mznc2016_probszephyrus14__8__6__3dzn.mps | 5 |  |
 |
| 193 | pegsolitaire | Hiroshige Dan | Model to solve model of a board game "Peg solitaire" | 1 |  |
 |
| 194 | pfour | MIPLIB submission pool | Imported from the MIPLIB2010 submissions. | 1 |  |
 |
| 195 | physiciansched | Pelin Damci-Kurt | Physician scheduling problem for hospitalist, radiology and kidney specialist groups. | 5 |  |
 |
| 196 | pigeon | Sam Allen | Model of 3D packing (container loading) problem | 5 |  |
 |
| 197 | piperout | Gleb Belov | Pipe routing with flexibility constraints. Models with _GCM in the name are simple routing | 5 |  |
 |
| 198 | pizza | Gleb Belov | These are the models from MiniZinc Challenges 2012-2016 (see www.minizinc.org), compiled for MIP WITH INDICATOR CONSTRAINTS using the develop branch of MiniZinc and CPLEX 12.7.1 on 30 April 2017. Thus, these models can only be handled by solvers accepting indicator constraints. For models compiled with big-M/domain decomposition only, see my previous submission to MIPLIB.To recompile, create a directory MODELS, a list lst12_16.txt of the models with full paths to mzn/dzn files of each model per line, and say$> ~/install/libmzn/tests/benchmarking/mzn-test.py -l ../lst12_16.txt -slvPrf MZN-CPLEX -debug 1 -addOption "-timeout 3 -D fIndConstr=true -D fMIPdomains=false" -useJoinedName "-writeModel MODELS_IND/%s.mps" Alternatively, you can compile individual model as follows: $> mzn-cplex -v -s -G linear -output-time ../challenge_2012_2016/mznc2016_probs/zephyrus/zephyrus.mzn ../challenge_2012_2016/mznc2016_p/zephyrus/14__8__6__3.dzn -a -timeout 3 -D fIndConstr=true -D fMIPdomains=false -writeModel MODELS_IND/challenge_2012_2016mznc2016_probszephyruszephyrusmzn-challenge_2012_2016mznc2016_probszephyrus14__8__6__3dzn.mps | 2 |  |
 |
| 199 | polygonpack | Antonio Frangioni | Given a set P of polygons, not necessarily convex, and a rectangle, we want to find the subset S of P with largest possible total area and a position every p in S so that there are no overlaps and they are all included in the rectangle. We allow a small set of rotations (0, 90, 180, 270 degrees) for every polygon. The problem is simplified w.r.t. the real application because the polygons do not have (fully encircled) "holes", which are supposedly filled-in separately, although they can have "bays". Models are saved as .lp. Model LpPackingModel_Dim means that we are trying to pack polygons taken from set ; there are currently 5 different sets, and is 7, 10 or 15. | 4 |  |
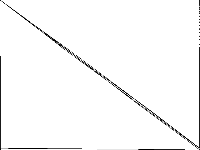 |
| 200 | pr_product | MIPLIB submission pool | Imported from the MIPLIB2010 submissions. | 4 |  |
 |
| 201 | proteindesign | Gleb Belov | Linearized Constraint Programming models of the MiniZinc Challenges 2012-2016. I should be able to produce versions with indicator constraints supported by Gurobi and CPLEX, however don't know if you can use them and if there is a standard format. These MPS were produced by Gurobi 7.0.2 using the MiniZinc develop branch on eb536656062ca13325a96b5d0881742c7d0e3c38 | 4 |  |
 |
| 202 | radiation | Gleb Belov | Linearized Constraint Programming models of the MiniZinc Challenges 2012-2016. I should be able to produce versions with indicator constraints supported by Gurobi and CPLEX, however don't know if you can use them and if there is a standard format. These MPS were produced by Gurobi 7.0.2 using the MiniZinc develop branch on eb536656062ca13325a96b5d0881742c7d0e3c38 | 2 | 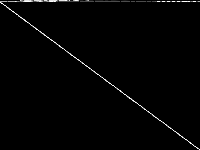 |
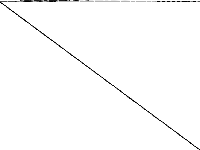 |
| 203 | rail0 | Thomas Schlechte | Track allocation problem modeled as arc coupling problem The problem was solved by CPLEX 12.4. It took approximately 170 hours. | 3 |  |
 |
| 204 | ran | J. Aronson | Fixed charge transportation problem | 3 |  |
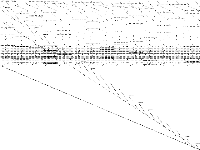 |
| 205 | reblock | Andreas Bley | Multi-period mine production scheduling model. Solved using ug[SCIP/spx], a distributed massively parallel version of SCIP run on 2,000 cores at the HLRN-II super computer facility. | 4 | 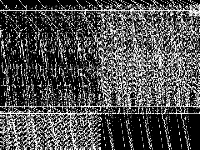 |
 |
| 206 | rmatr | Dmitry Krushinsky | Model coming from a formulation of the p-Median problem using square cost matrices | 5 |  |
 |
| 207 | rmine | Daniel Espinoza | Set of models comming from open pit minning over a cube and several time periods and two knapsack constraints per period | 4 |  |
 |
| 208 | rocI | Joerg Rambau | Optimal control model in the deterministic dynamic system given by bounded-confidence dynamics in a system of opinions | 5 |  |
 |
| 209 | rococo | A. Chabrier, E. Danna, C. Le Pape, L. Perron | Model for dimensioning the arc capacities in a telecommunication network. Solved by Gurobi 4.5.1 (4 threads) in 66892.47 seconds. | 5 |  |
 |
| 210 | rpp | Gleb Belov | These are the models from MiniZinc Challenges 2012-2016 (see www.minizinc.org), compiled for MIP WITH INDICATOR CONSTRAINTS using the develop branch of MiniZinc and CPLEX 12.7.1 on 30 April 2017. Thus, these models can only be handled by solvers accepting indicator constraints. For models compiled with big-M/domain decomposition only, see my previous submission to MIPLIB.To recompile, create a directory MODELS, a list lst12_16.txt of the models with full paths to mzn/dzn files of each model per line, and say$> ~/install/libmzn/tests/benchmarking/mzn-test.py -l ../lst12_16.txt -slvPrf MZN-CPLEX -debug 1 -addOption "-timeout 3 -D fIndConstr=true -D fMIPdomains=false" -useJoinedName "-writeModel MODELS_IND/%s.mps" Alternatively, you can compile individual model as follows: $> mzn-cplex -v -s -G linear -output-time ../challenge_2012_2016/mznc2016_probs/zephyrus/zephyrus.mzn ../challenge_2012_2016/mznc2016_p/zephyrus/14__8__6__3.dzn -a -timeout 3 -D fIndConstr=true -D fMIPdomains=false -writeModel MODELS_IND/challenge_2012_2016mznc2016_probszephyruszephyrusmzn-challenge_2012_2016mznc2016_probszephyrus14__8__6__3dzn.mps | 1 |  |
 |
| 211 | satellites | He Renjie | Ihe attachment is some models generated from real life satelliteschedule problem data,these models are easier comparable to real lifeproblem. The work is done by me and Alberto Ceselli from Univeristy ofMilano. I donnot know it is hard enough or not, if needs , I can generatemore difficult models. | 4 |  |
 |
| 212 | schedule | Simon Felix | Continuous-time project scheduling and selection, inspired by an industry use-case. Each project has a value, the sum should be maximized. Each project has a deadline, and an earliest start date. Three formulations of the same problem ("Pair A", "Pair B" and "Slot") - we expect "Pair B" to be the best formulation. | 5 |  |
 |
| 213 | scp | Shunji Umetani | This is a random test model generator for SCP using the scheme of the following paper, namely the column cost c[j] are integer randomly generated from [1,100]; every column covers at least one row; and every row is covered by at least two columns. see reference: E. Balas and A. Ho, Set covering algorithms using cutting planes, heuristics, and subgradient optimization: A computational study, Mathematical Programming, 12 (1980), 37-60. We have newly generated Classes I-N with the following parameter values, where each class has five models. We have also generated reduced models by a standard pricing method in the following paper: S. Umetani and M. Yagiura, Relaxation heuristics for the set covering problem, Journal of the Operations Research Society of Japan, 50 (2007), 350-375. You can obtain the model generator program from the following web site. https://sites.google.com/site/shunjiumetani/benchmark | 4 |  |
 |
| 214 | sct | Siemens | Assembly line balancing for printed circuit board production. First solved by Gurobi 7.0 in 65 hours (32 threads). | 5 |  |
 |
| 215 | selofsubspaces | Daniel Heinlein | Clique problems arising from a selection problem of subspaces in the PG(7,2) with different prescribed variables and numerically instable linear programming relaxation. | 1 |  |
 |
| 216 | seqsolve | Irv Lustig | The 3 problems in this group (seqsolve1-seqsolve3) represent a hierarchical optimization process, which is derived from a customer problem for assigning people to sites into blocks of time on days of the week. The specialty of this submission is that the best known solution for seqsolveX can be used as a MIP start for seqsolveX+1. For a description of the connections between the problems, please refer to the README.txt contained in the model data for this submission, which also includes MIP start files and a Gurobi log file. | 3 |  |
 |
| 217 | set3 | Kerem Akartunali | Multi-item lot-sizing with backlogging. Solved by SCIP 3.1.1 parallelized by UG 0.7.5 linked to CPLEX 12.6 as an LP solver on HLRN III (https://www.hlrn.de/home/view/System3/CrayHardware). Due to time limit restrictions, four repeated runs, each starting from the checkpointing file of the previous run, were done. Each run had a time limit of 12 hours while using 6144 (runs 1) or 3072 cores (run 2 - 4). | 1 |  |
 |
| 218 | shiftreg | Domenico Salvagnin | Multi-activity shift scheduling problem with 1 activity and 12 employees, using an implicit model based on a regular language. | 3 | 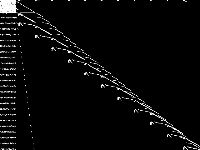 |
 |
| 219 | shipschedule | Gleb Belov | These are the models from MiniZinc Challenges 2012-2016 (see www.minizinc.org), compiled for MIP WITH INDICATOR CONSTRAINTS using the develop branch of MiniZinc and CPLEX 12.7.1 on 30 April 2017. Thus, these models can only be handled by solvers accepting indicator constraints. For models compiled with big-M/domain decomposition only, see my previous submission to MIPLIB.To recompile, create a directory MODELS, a list lst12_16.txt of the models with full paths to mzn/dzn files of each model per line, and say$> ~/install/libmzn/tests/benchmarking/mzn-test.py -l ../lst12_16.txt -slvPrf MZN-CPLEX -debug 1 -addOption "-timeout 3 -D fIndConstr=true -D fMIPdomains=false" -useJoinedName "-writeModel MODELS_IND/%s.mps" Alternatively, you can compile individual model as follows: $> mzn-cplex -v -s -G linear -output-time ../challenge_2012_2016/mznc2016_probs/zephyrus/zephyrus.mzn ../challenge_2012_2016/mznc2016_p/zephyrus/14__8__6__3.dzn -a -timeout 3 -D fIndConstr=true -D fMIPdomains=false -writeModel MODELS_IND/challenge_2012_2016mznc2016_probszephyruszephyrusmzn-challenge_2012_2016mznc2016_probszephyrus14__8__6__3dzn.mps | 3 |  |
 |
| 220 | shs | Christoph Helmberg | Joint online truck scheduling and inventory management for multiple warehouses. | 3 | 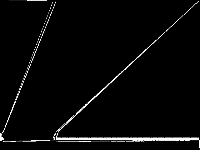 |
 |
| 221 | sing | Daniel Espinoza | Imported from the MIPLIB2010 submissions. | 5 |  |
 |
| 222 | SiweiSun | Siwei Sun | These models come from my cryptographic research and are used to search for the best differential characteristics of the round-reduced versions of the block cipher Serpent with the mixed-integer programming technique. For all the models, including S1234.lp, S56701.lp, S456701.lp, I have found a feasible solution in the corresponding mst file. The challenge is that can we find better solutions or can we find the best solutions. | 1 |  |
 |
| 223 | sp_product | MIPLIB submission pool | Imported from the MIPLIB2010 submissions. | 1 |  |
 |
| 224 | sp9 | J. Goessens, S. v. Hoessel, L. Kroon | Railway line planning model | 5 |  |
 |
| 225 | Spinoza | Daniel Espinoza | Wine Scheduling problem with 82 jobs and four processing machines | 4 |  |
 |
| 226 | splice | Gleb Belov | Linearized Constraint Programming models of the MiniZinc Challenges 2012-2016. I should be able to produce versions with indicator constraints supported by Gurobi and CPLEX, however don't know if you can use them and if there is a standard format. These MPS were produced by Gurobi 7.0.2 using the MiniZinc develop branch on eb536656062ca13325a96b5d0881742c7d0e3c38 | 2 | 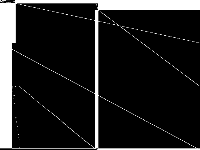 |
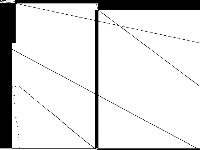 |
| 227 | square | Sascha Kurz | Squaring the square For a given integer n, determine the minimum number of squares in a tiling of an \\(n\\times n\\) square using using only integer sided squares of smaller size. (Although the models get quite large even for moderate n, they can be solved to optimality for all \\(n \\le 61\\), while challenging the MIP solver, especially the presolver.) | 5 | 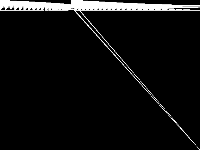 |
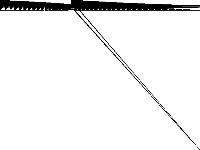 |
| 228 | stein | MIPLIB submission pool | Imported from the MIPLIB2010 submissions. | 3 |  |
 |
| 229 | supplynetworkplanning | Gerald Gamrath | Supply network planning problems. | 5 |  |
 |
| 230 | supportvectormachine | Toni Sorrell | Suport vector machine with ramp loss. GSVM2-RL is the formulation found in Hess E. and Brooks P. (2015) paper, The Support Vector Machine and Mixed Integer Linear Programming: Ramp Loss SVM with L1-Norm Regularization | 4 |  |
 |
| 231 | swath | D. Panton | Model arising from the defense industry, involves planning missions for radar surveillance. John Forrest and Laszlo Ladanyi solved this model by reformulation in 1999. Alkis Vazacopoulos reports solving this model using XPRESS 2006B. | 4 |  |
 |
| 232 | timetabling | George Fonseca | Educational timetabling problems from several real schools/universities around the world. These models were originally expressed in the xhstt file format [1] and formulated as Integer Programming models as described at [2]. | 4 |  |
 |
| 233 | timtab | C. Liebchen, R. Möhring | Public transport scheduling problem | 2 |  |
 |
| 234 | traininstance | Gleb Belov | Linearized Constraint Programming models of the MiniZinc Challenges 2012-2016. I should be able to produce versions with indicator constraints supported by Gurobi and CPLEX, however don't know if you can use them and if there is a standard format. These MPS were produced by Gurobi 7.0.2 using the MiniZinc develop branch on eb536656062ca13325a96b5d0881742c7d0e3c38 | 2 |  |
 |
| 235 | triptim | MIPLIB submission pool | Imported from the MIPLIB2010 submissions. | 4 |  |
 |
| 236 | uccase | Daniel Espinoza | Imported from the MIPLIB2010 submissions. | 5 |  |
 |
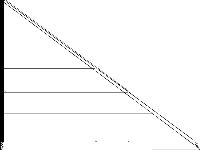
| 237 | ustun | Berk Ustun | MIP to create optimized data-driven scoring systems. See: https://github.com/ustunb/miplib2017-slim#miplib2017-slim for a description. | 3 | 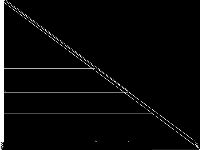 |
 |
| 238 | vrp | Gleb Belov | These are the models from MiniZinc Challenges 2012-2016 (see www.minizinc.org), compiled for MIP WITH INDICATOR CONSTRAINTS using the develop branch of MiniZinc and CPLEX 12.7.1 on 30 April 2017. Thus, these models can only be handled by solvers accepting indicator constraints. For models compiled with big-M/domain decomposition only, see my previous submission to MIPLIB.To recompile, create a directory MODELS, a list lst12_16.txt of the models with full paths to mzn/dzn files of each model per line, and say$> ~/install/libmzn/tests/benchmarking/mzn-test.py -l ../lst12_16.txt -slvPrf MZN-CPLEX -debug 1 -addOption "-timeout 3 -D fIndConstr=true -D fMIPdomains=false" -useJoinedName "-writeModel MODELS_IND/%s.mps" Alternatively, you can compile individual model as follows: $> mzn-cplex -v -s -G linear -output-time ../challenge_2012_2016/mznc2016_probs/zephyrus/zephyrus.mzn ../challenge_2012_2016/mznc2016_p/zephyrus/14__8__6__3.dzn -a -timeout 3 -D fIndConstr=true -D fMIPdomains=false -writeModel MODELS_IND/challenge_2012_2016mznc2016_probszephyruszephyrusmzn-challenge_2012_2016mznc2016_probszephyrus14__8__6__3dzn.mps | 4 |  |
 |

