×
![]()
rococoC12-010001: Instance-to-Instance Comparison Results
| Type: | Instance |
| Submitter: | A. Chabrier, E. Danna, C. Le Pape, L. Perron |
| Description: | Model for dimensioning the arc capacities in a telecommunication network. |
| MIPLIB Entry |
Parent Instance (rococoC12-010001)
All other instances below were be compared against this "query" instance.  |
 |
 |
 |
 |
 |
|
Raw
This is the CCM image before the decomposition procedure has been applied.
|
Decomposed
This is the CCM image after a decomposition procedure has been applied. This is the image used by the MIC's image-based comparisons for this query instance.
|
Composite of MIC Top 5
Composite of the five decomposed CCM images from the MIC Top 5.
|
Composite of MIPLIB Top 5
Composite of the five decomposed CCM images from the MIPLIB Top 5.
|
Model Group Composite Image
Composite of the decomposed CCM images for every instance in the same model group as this query.
|
MIC Top 5 Instances
These are the 5 decomposed CCM images that are most similar to decomposed CCM image for the the query instance, according to the ISS metric.  |
Decomposed
These decomposed images were created by GCG.
|
 |
 |
 |
 |
 |
| Name | rococoC11-010100 [MIPLIB] | tbfp-bigm [MIPLIB] | polygonpack4-15 [MIPLIB] | polygonpack4-7 [MIPLIB] | polygonpack4-10 [MIPLIB] | |
|
Rank / ISS
The image-based structural similarity (ISS) metric measures the Euclidean distance between the image-based feature vectors for the query instance and all other instances. A smaller ISS value indicates greater similarity.
|
1 / 0.644 | 2 / 0.749 | 3 / 0.761 | 4 / 0.822 | 5 / 0.824 | |
|
Raw
These images represent the CCM images in their raw forms (before any decomposition was applied) for the MIC top 5.
|
 |
 |
 |
 |
 |
MIPLIB Top 5 Instances
These are the 5 instances that are most closely related to the query instance, according to the instance statistic-based similarity measure employed by MIPLIB 2017  |
Decomposed
These decomposed images were created by GCG.
|
 |
 |
 |
 |
 |
| Name | rococoC11-010100 [MIPLIB] | rococoB10-011000 [MIPLIB] | rococoC10-001000 [MIPLIB] | rococoC11-011100 [MIPLIB] | neos-826650 [MIPLIB] | |
|
Rank / ISS
The image-based structural similarity (ISS) metric measures the Euclidean distance between the image-based feature vectors for the query instance and all model groups. A smaller ISS value indicates greater similarity.
|
1 / 0.644 | 18 / 0.994 | 56 / 1.119 | 86 / 1.162 | 813 / 2.253 | |
|
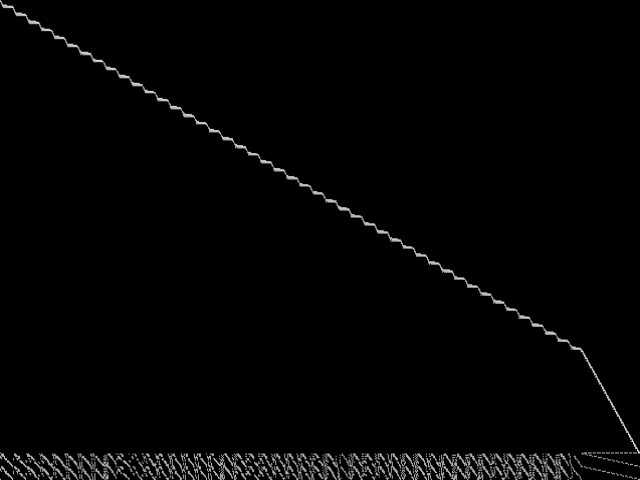
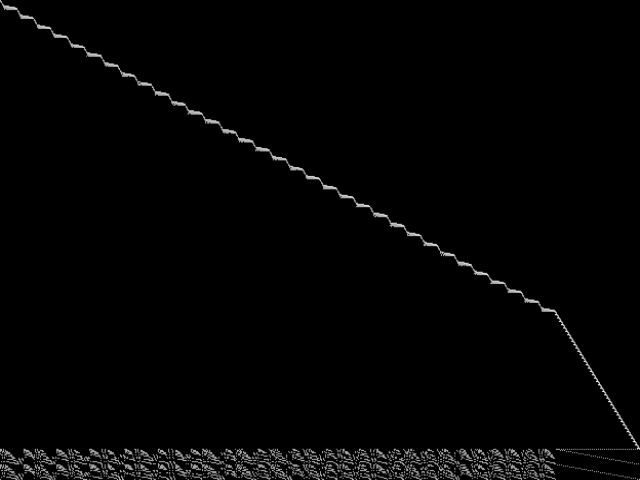
Raw
These images represent the CCM images in their raw forms (before any decomposition was applied) for the MIPLIB top 5.
|
 |
 |
 |
 |
 |
Instance Summary
The table below contains summary information for rococoC12-010001, the five most similar instances to rococoC12-010001 according to the MIC, and the five most similar instances to rococoC12-010001 according to MIPLIB 2017.
| INSTANCE | SUBMITTER | DESCRIPTION | ISS | RANK | |
|---|---|---|---|---|---|
| Parent Instance | rococoC12-010001 [MIPLIB] | A. Chabrier, E. Danna, C. Le Pape, L. Perron | Model for dimensioning the arc capacities in a telecommunication network. | 0.000000 | - |
| MIC Top 5 | rococoC11-010100 [MIPLIB] | A. Chabrier, E. Danna, C. Le Pape, L. Perron | Model for dimensioning the arc capacities in a telecommunication network. | 0.644174 | 1 |
| tbfp-bigm [MIPLIB] | Rob Pratt | Two formulations (big-M and network-based) for traveling baseball fan problem. Uses data from 2014 Major League Baseball regular season. Paper uses 2014 data: http://support.sas.com/resources/papers/proceedings14/SAS101-2014.pdf Blog post uses 2015 data: http://blogs.sas.com/content/operations/2015/04/03/the-traveling-baseball-fan-problem/ | 0.749019 | 2 | |
| polygonpack4-15 [MIPLIB] | Antonio Frangioni | Given a set P of polygons, not necessarily convex, and a rectangle, we want to find the subset S of P with largest possible total area and a position every p in S so that there are no overlaps and they are all included in the rectangle. We allow a small set of rotations (0, 90, 180, 270 degrees) for every polygon. The problem is simplified w.r.t. the real application because the polygons do not have (fully encircled) "holes", which are supposedly filled-in separately, although they can have "bays". Models are saved as .lp. Instance LpPackingModel_Dim means that we are trying to pack polygons taken from set ; there are currently 5 different sets, and is 7, 10 or 15. | 0.760713 | 3 | |
| polygonpack4-7 [MIPLIB] | Antonio Frangioni | Given a set P of polygons, not necessarily convex, and a rectangle, we want to find the subset S of P with largest possible total area and a position every p in S so that there are no overlaps and they are all included in the rectangle. We allow a small set of rotations (0, 90, 180, 270 degrees) for every polygon. The problem is simplified w.r.t. the real application because the polygons do not have (fully encircled) "holes", which are supposedly filled-in separately, although they can have "bays". Models are saved as .lp. Instance LpPackingModel_Dim means that we are trying to pack polygons taken from set ; there are currently 5 different sets, and is 7, 10 or 15. | 0.821885 | 4 | |
| polygonpack4-10 [MIPLIB] | Antonio Frangioni | Given a set P of polygons, not necessarily convex, and a rectangle, we want to find the subset S of P with largest possible total area and a position every p in S so that there are no overlaps and they are all included in the rectangle. We allow a small set of rotations (0, 90, 180, 270 degrees) for every polygon. The problem is simplified w.r.t. the real application because the polygons do not have (fully encircled) "holes", which are supposedly filled-in separately, although they can have "bays". Models are saved as .lp. Instance LpPackingModel_Dim means that we are trying to pack polygons taken from set ; there are currently 5 different sets, and is 7, 10 or 15. | 0.823517 | 5 | |
| MIPLIB Top 5 | rococoC11-010100 [MIPLIB] | A. Chabrier, E. Danna, C. Le Pape, L. Perron | Model for dimensioning the arc capacities in a telecommunication network. | 0.644174 | 1 |
| rococoB10-011000 [MIPLIB] | A. Chabrier, E. Danna, C. Le Pape, L. Perron | Model for dimensioning the arc capacities in a telecommunication network | 0.994372 | 18 | |
| rococoC10-001000 [MIPLIB] | A. Chabrier, E. Danna, C. Le Pape, L. Perron | Model for dimensioning the arc capacities in a telecommunication network | 1.119321 | 56 | |
| rococoC11-011100 [MIPLIB] | A. Chabrier, E. Danna, C. Le Pape, L. Perron | Model for dimensioning the arc capacities in a telecommunication network. Solved by Gurobi 4.5.1 (4 threads) in 66892.47 seconds. | 1.161886 | 86 | |
| neos-826650 [MIPLIB] | NEOS Server Submission | Instance coming from the NEOS Server with unknown application | 2.253168 | 813 |
rococoC12-010001: Instance-to-Model Comparison Results
| Model Group Assignment from MIPLIB: | rococo |
| Assigned Model Group Rank/ISS in the MIC: | 6 / 1.593 |
MIC Top 5 Model Groups
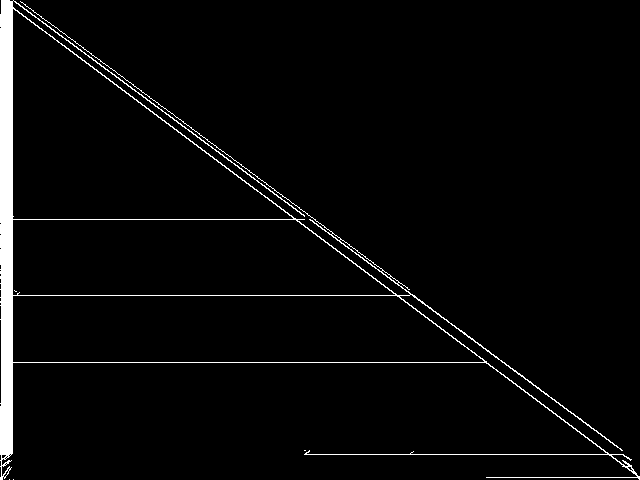
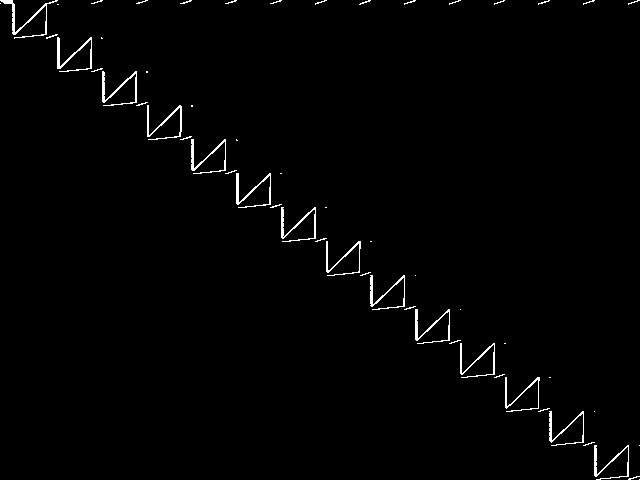
These are the 5 model group composite (MGC) images that are most similar to the decomposed CCM image for the query instance, according to the ISS metric.  |
These are model group composite (MGC) images for the MIC top 5 model groups.
|
 |
 |
 |
 |
 |
| Name | polygonpack | ustun | rmatr | map | allcolor | |
|
Rank / ISS
The image-based structural similarity (ISS) metric measures the Euclidean distance between the image-based feature vectors for the query instance and all other instances. A smaller ISS value indicates greater similarity.
|
1 / 1.324 | 2 / 1.356 | 3 / 1.361 | 4 / 1.362 | 5 / 1.550 |
Model Group Summary
The table below contains summary information for the five most similar model groups to rococoC12-010001 according to the MIC.
| MODEL GROUP | SUBMITTER | DESCRIPTION | ISS | RANK | |
|---|---|---|---|---|---|
| MIC Top 5 | polygonpack | Antonio Frangioni | Given a set P of polygons, not necessarily convex, and a rectangle, we want to find the subset S of P with largest possible total area and a position every p in S so that there are no overlaps and they are all included in the rectangle. We allow a small set of rotations (0, 90, 180, 270 degrees) for every polygon. The problem is simplified w.r.t. the real application because the polygons do not have (fully encircled) "holes", which are supposedly filled-in separately, although they can have "bays". Models are saved as .lp. Model LpPackingModel_Dim means that we are trying to pack polygons taken from set ; there are currently 5 different sets, and is 7, 10 or 15. | 1.324310 | 1 |
| ustun | Berk Ustun | MIP to create optimized data-driven scoring systems. See: https://github.com/ustunb/miplib2017-slim#miplib2017-slim for a description. | 1.355728 | 2 | |
| rmatr | Dmitry Krushinsky | Model coming from a formulation of the p-Median problem using square cost matrices | 1.360605 | 3 | |
| map | Kiyan Ahmadizadeh | Land parcel selection problems motivated by Red-Cockaded Woodpecker conservation problem | 1.361727 | 4 | |
| allcolor | Domenico Salvagnin | Prepack optimization model. | 1.549908 | 5 |

