×
![]()
neos-pseudoapplication-102
| Type: | Model Group |
| Submitter: | Hans Mittelmann |
| Description: | Seem to be VRP output from 2-hour runs of Gurobi on 12 threads is included |
Parent Model Group (neos-pseudoapplication-102)
All other model groups below were be compared against this "query" model group.  |
 |
|
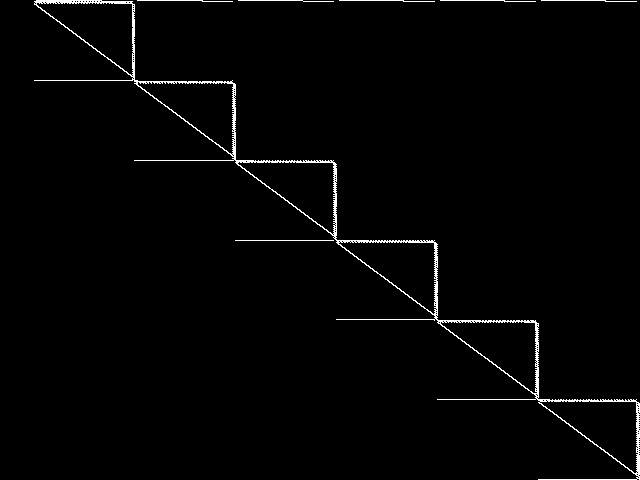
Model Group Composite (MGC) image
Composite of the decomposed CCM images for every instance in the query model group.
|
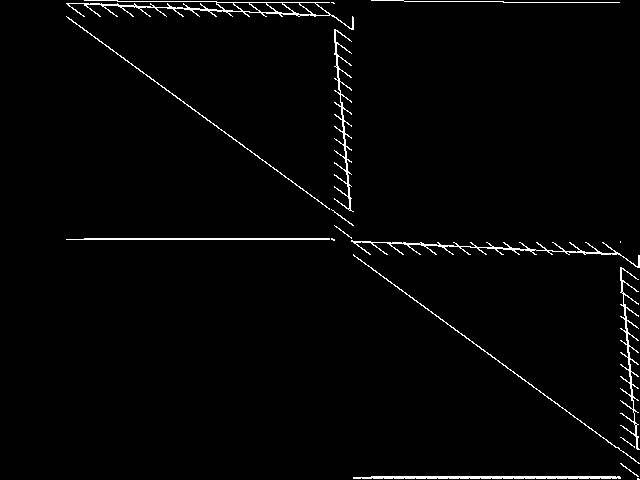
Component Instances (Decomposed)
These are the decomposed CCM images for each instance in the query model group.  |
These are component instance images.
|
 |
 |
 |
 |
 |
| Name | neos-5266653-tugela | neos-5261882-treska | neos-1456979 | ns1905797 | neos-5260764-orauea |
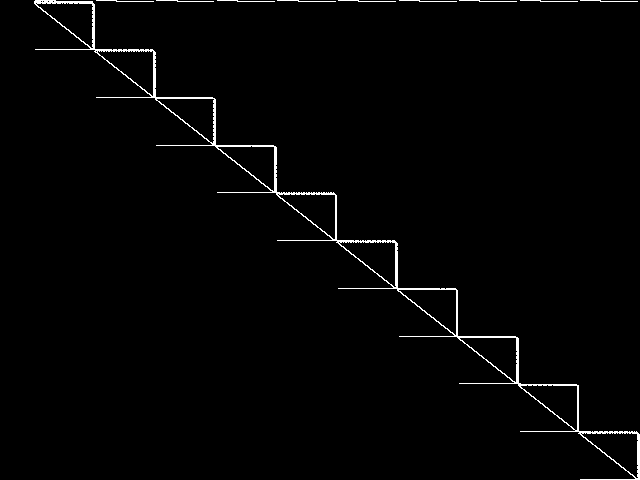
MIC Top 5 Model Groups
These are the 5 MGC images that are most similar to the MGC image for the query model group, according to the ISS metric.  |
FIXME - These are model group composite images.
|
 |
 |
 |
 |
 |
| Name | cvs | neos-pseudoapplication-50 | neos-pseudoapplication-9 | fastxgemm | neos-pseudoapplication-14 | |
|
Rank / ISS
The image-based structural similarity (ISS) metric measures the Euclidean distance between the image-based feature vectors for the query model group and all other model groups. A smaller ISS value indicates greater similarity.
|
1 / 1.883 | 2 / 1.928 | 3 / 1.932 | 4 / 1.950 | 5 / 2.012 |
Model Group Summary
The table below contains summary information for neos-pseudoapplication-102, and for the five most similar model groups to neos-pseudoapplication-102 according to the MIC.
| MODEL GROUP | SUBMITTER | DESCRIPTION | ISS | RANK | |
|---|---|---|---|---|---|
| Parent Model Group | neos-pseudoapplication-102 | Hans Mittelmann | Seem to be VRP output from 2-hour runs of Gurobi on 12 threads is included | 0.000000 | - |
| MIC Top 5 | cvs | Michael Bastubbe | Capacitated vertex separator problem on randomly generated hypergraph with 128 vertices and 89 hyperedges in at most 16 components each including at most 8 vertices. solved with default GCG/Soplex in about 2000 seconds. | 1.883262 | 1 |
| neos-pseudoapplication-50 | NEOS Server Submission | Model coming from the NEOS Server with unknown application | 1.927924 | 2 | |
| neos-pseudoapplication-9 | NEOS Server Submission | Model coming from the NEOS Server with unknown application. | 1.931920 | 3 | |
| fastxgemm | Laurent Sorber | Naive multiplication of two N by N matrices requires N^3 scalar multiplications. For N=2, Strassen showed that it could be done in only R=7 < 8=N^3 multiplications. For N=3, it is known that 19 <= R <= 23, and for N=4 it is known that 34 <= R <= 49. This repository contains code that generates a mixed-integer linear program (MILP) formulation of the fast matrix multiplication problem for finding solutions with R < N^3 and proving that they are optimal. For a more detailed description, see the accompanying manuscript. | 1.949863 | 4 | |
| neos-pseudoapplication-14 | Jeff Linderoth | (None provided) | 2.012193 | 5 |

