×
![]()
neos-pseudoapplication-30
| Type: | Model Group |
| Submitter: | Jeff Linderoth |
| Description: | (None provided) |
Parent Model Group (neos-pseudoapplication-30)
All other model groups below were be compared against this "query" model group.  |
 |
|
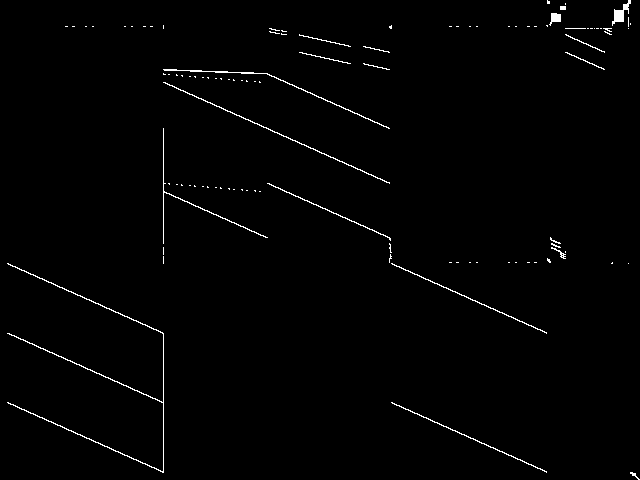
Model Group Composite (MGC) image
Composite of the decomposed CCM images for every instance in the query model group.
|
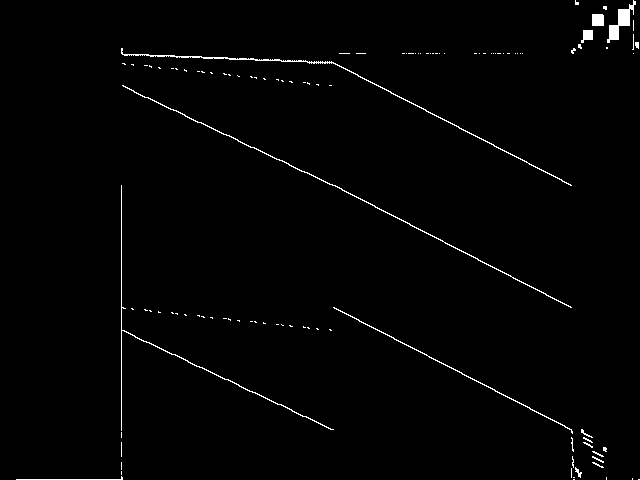
Component Instances (Decomposed)
These are the decomposed CCM images for each instance in the query model group.  |
These are component instance images.
|
 |
 |
 |
 |
 |
| Name | neos-4260495-otere | neos-4805882-barwon | neos-4306827-ravan | neos-4724674-aorere | neos-4722843-widden |
MIC Top 5 Model Groups
These are the 5 MGC images that are most similar to the MGC image for the query model group, according to the ISS metric.  |
FIXME - These are model group composite images.
|
 |
 |
 |
 |
 |
| Name | assign1 | independentset | f2gap | 2hopcds | generated | |
|
Rank / ISS
The image-based structural similarity (ISS) metric measures the Euclidean distance between the image-based feature vectors for the query model group and all other model groups. A smaller ISS value indicates greater similarity.
|
1 / 1.896 | 2 / 1.912 | 3 / 1.915 | 4 / 1.925 | 5 / 1.955 |
Model Group Summary
The table below contains summary information for neos-pseudoapplication-30, and for the five most similar model groups to neos-pseudoapplication-30 according to the MIC.
| MODEL GROUP | SUBMITTER | DESCRIPTION | ISS | RANK | |
|---|---|---|---|---|---|
| Parent Model Group | neos-pseudoapplication-30 | Jeff Linderoth | (None provided) | 0.000000 | - |
| MIC Top 5 | assign1 | Robert Fourer | Imported from the MIPLIB2010 submissions. | 1.895868 | 1 |
| independentset | Toni Sorrell | These models are based on Neil Sloane's Challenge problems: Independent Sets in Graphs. | 1.912428 | 2 | |
| f2gap | Salim Haddadi | Restrictions of well-known hard generalized assignment problem models (D10400,D20400,D40400,D15900,D30900,D60900,D201600,D401600,D801600) | 1.915137 | 3 | |
| 2hopcds | Austin Buchanan | A problem in wireless networks. The objective is to select a minimum number of relay nodes so that any two nonadjacent nodes can communicate by way of the chosen relay nodes in at most s hops, where s is a problem input. The 2-hop case of this problem can be formulated as a set cover/hitting set problem with n binary variables and n^2 constraints: _{ k N(i) N(j) } x_k 1 for nonadjacent node pairs {i,j}. Despite the formulation's simplicity, models with as few as 120 variables are left unsolved after one hour using Gurobi 7.0.2. | 1.925091 | 4 | |
| generated | Simon Bowly | Randomly generated integer and binary programming models. These results are part of an early phase of work aimed at generating diverse and challenging MIP models for experimental testing. We have aimed to produce small integer and binary programming models which are reasonably difficult to solve and have varied structure, eliciting a range of behaviour in state of the art algorithms. | 1.955130 | 5 |

