×
![]()
neos-pseudoapplication-52
| Type: | Model Group |
| Submitter: | Jeff Linderoth |
| Description: | (None provided) |
Parent Model Group (neos-pseudoapplication-52)
All other model groups below were be compared against this "query" model group.  |
 |
|
Model Group Composite (MGC) image
Composite of the decomposed CCM images for every instance in the query model group.
|
Component Instances (Decomposed)
These are the decomposed CCM images for each instance in the query model group.  |
These are component instance images.
|
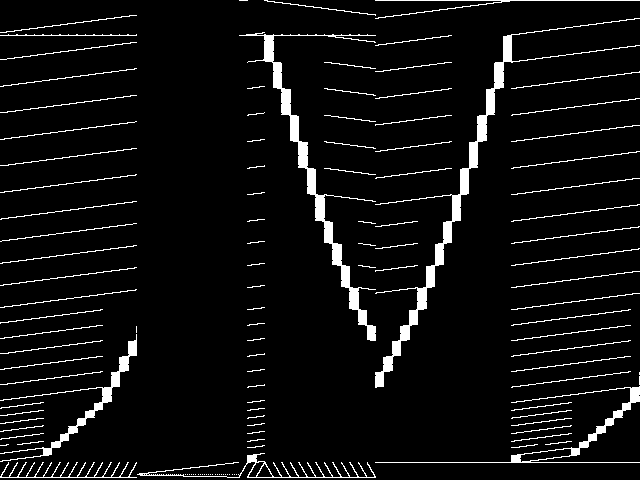 |
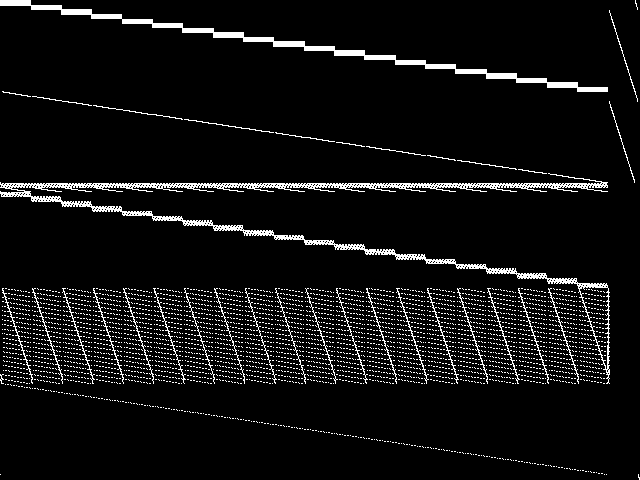 |
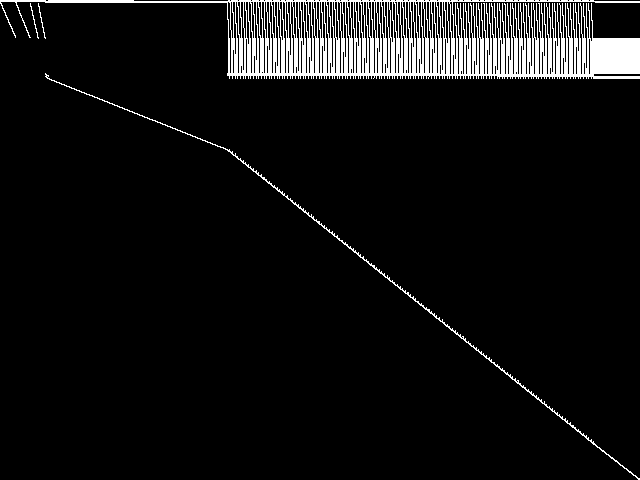 |
 |
 |
| Name | neos-3355120-tarago | ns1456591 | neos-2669500-cust | neos-2746589-doon |
MIC Top 5 Model Groups
These are the 5 MGC images that are most similar to the MGC image for the query model group, according to the ISS metric.  |
FIXME - These are model group composite images.
|
 |
 |
 |
 |
 |
| Name | iis | neos-pseudoapplication-106 | 2hopcds | neos-pseudoapplication-78 | neos-pseudoapplication-103 | |
|
Rank / ISS
The image-based structural similarity (ISS) metric measures the Euclidean distance between the image-based feature vectors for the query model group and all other model groups. A smaller ISS value indicates greater similarity.
|
1 / 1.371 | 2 / 1.432 | 3 / 1.442 | 4 / 1.501 | 5 / 1.601 |
Model Group Summary
The table below contains summary information for neos-pseudoapplication-52, and for the five most similar model groups to neos-pseudoapplication-52 according to the MIC.
| MODEL GROUP | SUBMITTER | DESCRIPTION | ISS | RANK | |
|---|---|---|---|---|---|
| Parent Model Group | neos-pseudoapplication-52 | Jeff Linderoth | (None provided) | 0.000000 | - |
| MIC Top 5 | iis | Marc Pfetsch | 23 "middlehard" Set-Covering Models for MIPLIB: they have a small number of variables compared to the number of constraints and CPLEX 12.1 needs about one hour to solve them.For more information, have a look into the readme file which explains how the models can be created. | 1.370753 | 1 |
| neos-pseudoapplication-106 | Hans Mittelmann | Collection of anonymous submissions to the NEOS Server for Optimization | 1.431559 | 2 | |
| 2hopcds | Austin Buchanan | A problem in wireless networks. The objective is to select a minimum number of relay nodes so that any two nonadjacent nodes can communicate by way of the chosen relay nodes in at most s hops, where s is a problem input. The 2-hop case of this problem can be formulated as a set cover/hitting set problem with n binary variables and n^2 constraints: _{ k N(i) N(j) } x_k 1 for nonadjacent node pairs {i,j}. Despite the formulation's simplicity, models with as few as 120 variables are left unsolved after one hour using Gurobi 7.0.2. | 1.442470 | 3 | |
| neos-pseudoapplication-78 | Jeff Linderoth | (None provided) | 1.500660 | 4 | |
| neos-pseudoapplication-103 | Hans Mittelmann | Collection of anonymous submissions to the NEOS Server for Optimization | 1.601443 | 5 |

