×
![]()
8div-n59k10: Instance-to-Instance Comparison Results
| Type: | Instance |
| Submitter: | Sascha Kurz |
| Description: | Projective binary 8-divisible linear block codes A linear block code is called 8-divisible if the weights of its codewords are divisible by 8. It is called projective if there are no duplicate columns in the generator matrix. The possible lengths of 8-divisible linear block codes have been classified except for length n=59, where it is undecided whether such a linear code exists. The possible dimensions satisfy \\(10 \\le k \\le 20\\). Instance 8div_n59_kXX contains the corresponding feasibility problem. Projective binary 8-divisible linear block codes occur as hole configurations of so-called partial solid spreads in finite geometry. Binary 4-divisible linear block codes have applications in physics. |
| MIPLIB Entry |
Parent Instance (8div-n59k10)
All other instances below were be compared against this "query" instance.  |
 |
 |
 |
 |
 |
|
Raw
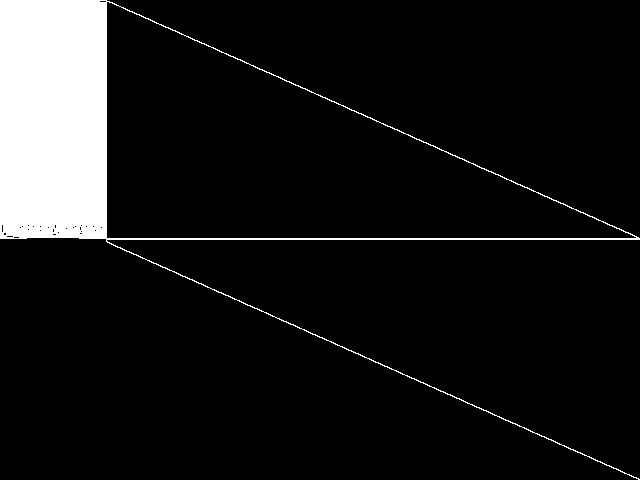
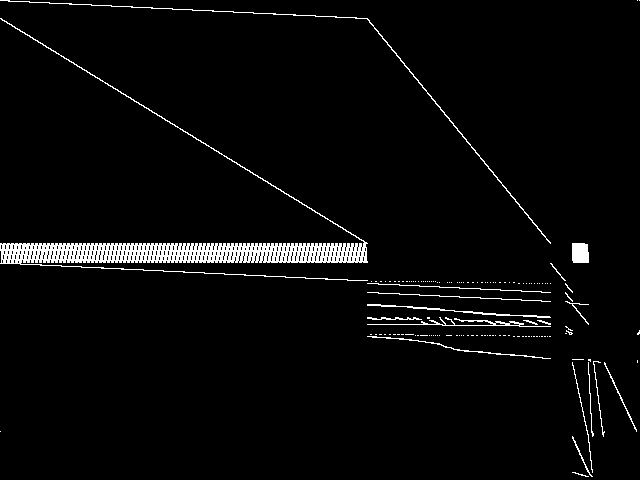
This is the CCM image before the decomposition procedure has been applied.
|
Decomposed
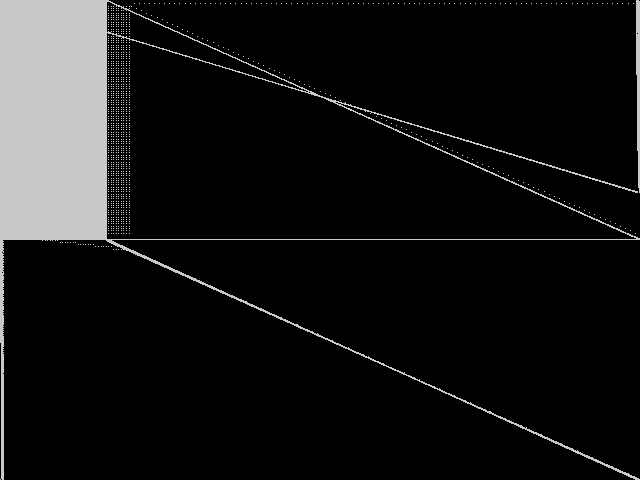
This is the CCM image after a decomposition procedure has been applied. This is the image used by the MIC's image-based comparisons for this query instance.
|
Composite of MIC Top 5
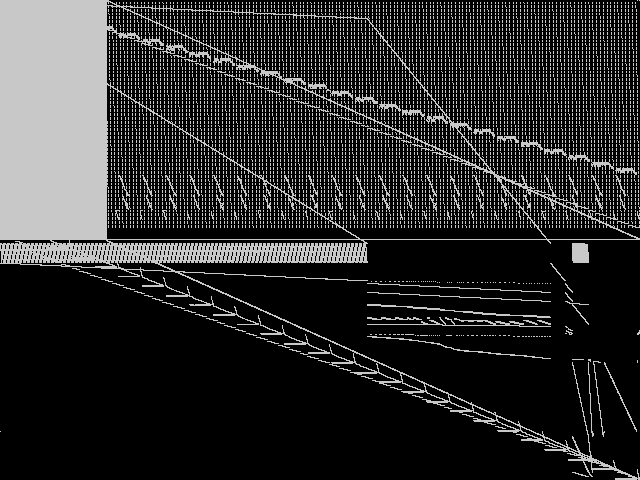
Composite of the five decomposed CCM images from the MIC Top 5.
|
Composite of MIPLIB Top 5
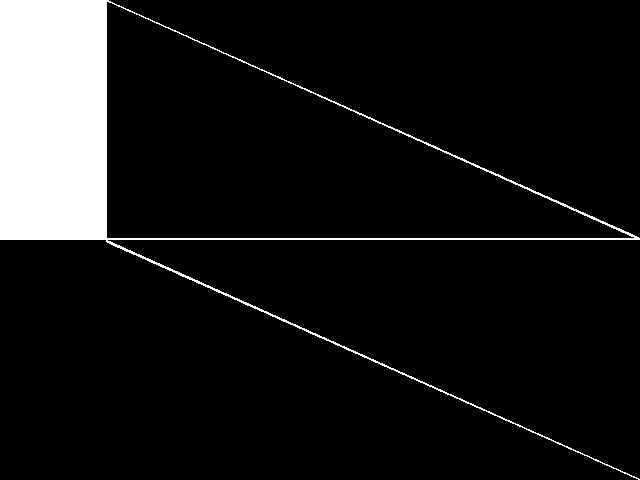
Composite of the five decomposed CCM images from the MIPLIB Top 5.
|
Model Group Composite Image
Composite of the decomposed CCM images for every instance in the same model group as this query.
|
MIC Top 5 Instances
These are the 5 decomposed CCM images that are most similar to decomposed CCM image for the the query instance, according to the ISS metric.  |
Decomposed
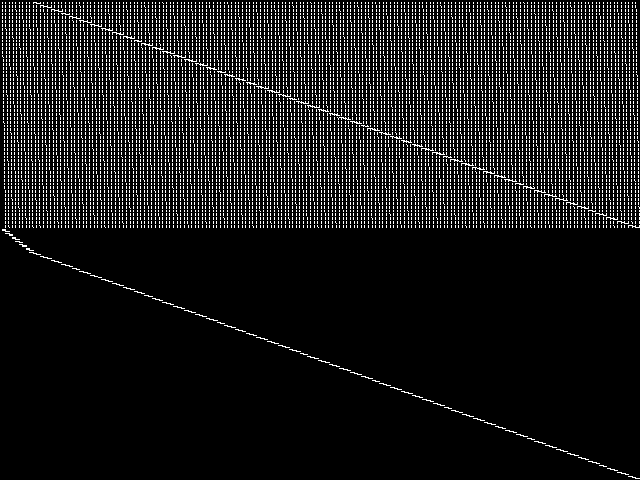
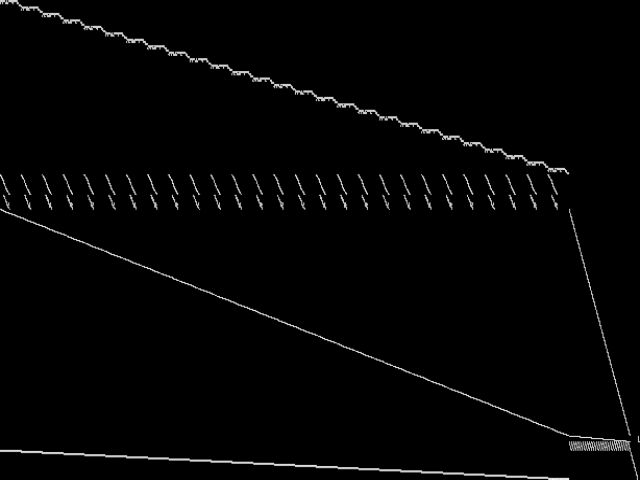
These decomposed images were created by GCG.
|
 |
 |
 |
 |
 |
| Name | 8div-n59k11 [MIPLIB] | 8div-n59k12 [MIPLIB] | prod1 [MIPLIB] | fhnw-schedule-pairb400 [MIPLIB] | fhnw-schedule-pairb200 [MIPLIB] | |
|
Rank / ISS
The image-based structural similarity (ISS) metric measures the Euclidean distance between the image-based feature vectors for the query instance and all other instances. A smaller ISS value indicates greater similarity.
|
1 / 0.258 | 2 / 0.259 | 3 / 0.653 | 4 / 0.846 | 5 / 0.894 | |
|
Raw
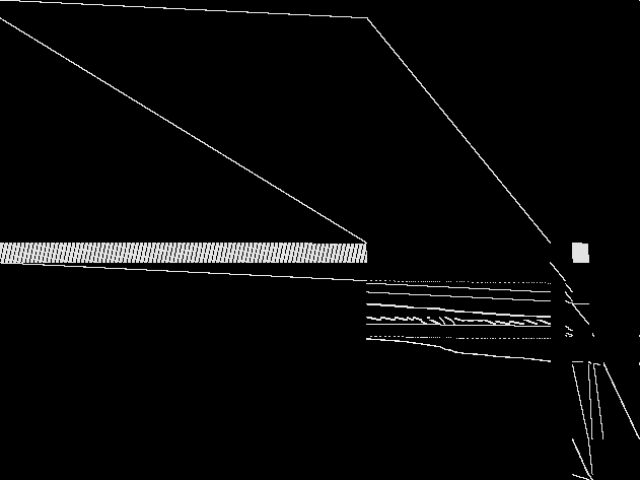
These images represent the CCM images in their raw forms (before any decomposition was applied) for the MIC top 5.
|
 |
 |
 |
 |
 |
MIPLIB Top 5 Instances
These are the 5 instances that are most closely related to the query instance, according to the instance statistic-based similarity measure employed by MIPLIB 2017  |
Decomposed
These decomposed images were created by GCG.
|
 |
 |
 |
 |
 |
| Name | 8div-n59k11 [MIPLIB] | 8div-n59k12 [MIPLIB] | neos-3045796-mogo [MIPLIB] | brazil3 [MIPLIB] | neos-952987 [MIPLIB] | |
|
Rank / ISS
The image-based structural similarity (ISS) metric measures the Euclidean distance between the image-based feature vectors for the query instance and all model groups. A smaller ISS value indicates greater similarity.
|
1 / 0.258 | 2 / 0.259 | 379 / 1.491 | 496 / 1.576 | 742 / 1.867 | |
|
Raw
These images represent the CCM images in their raw forms (before any decomposition was applied) for the MIPLIB top 5.
|
 |
 |
 |
 |
 |
Instance Summary
The table below contains summary information for 8div-n59k10, the five most similar instances to 8div-n59k10 according to the MIC, and the five most similar instances to 8div-n59k10 according to MIPLIB 2017.
| INSTANCE | SUBMITTER | DESCRIPTION | ISS | RANK | |
|---|---|---|---|---|---|
| Parent Instance | 8div-n59k10 [MIPLIB] | Sascha Kurz | Projective binary 8-divisible linear block codes A linear block code is called 8-divisible if the weights of its codewords are divisible by 8. It is called projective if there are no duplicate columns in the generator matrix. The possible lengths of 8-divisible linear block codes have been classified except for length n=59, where it is undecided whether such a linear code exists. The possible dimensions satisfy \\(10 \\le k \\le 20\\). Instance 8div_n59_kXX contains the corresponding feasibility problem. Projective binary 8-divisible linear block codes occur as hole configurations of so-called partial solid spreads in finite geometry. Binary 4-divisible linear block codes have applications in physics. | 0.000000 | - |
| MIC Top 5 | 8div-n59k11 [MIPLIB] | Sascha Kurz | Projective binary 8-divisible linear block codes A linear block code is called 8-divisible if the weights of its codewords are divisible by 8. It is called projective if there are no duplicate columns in the generator matrix. The possible lengths of 8-divisible linear block codes have been classified except for length n=59, where it is undecided whether such a linear code exists. The possible dimensions satisfy \\(10 \\le k \\le 20\\). Instance 8div_n59_kXX contains the corresponding feasibility problem. Projective binary 8-divisible linear block codes occur as hole configurations of so-called partial solid spreads in finite geometry. Binary 4-divisible linear block codes have applications in physics. | 0.258109 | 1 |
| 8div-n59k12 [MIPLIB] | Sascha Kurz | Projective binary 8-divisible linear block codes A linear block code is called 8-divisible if the weights of its codewords are divisible by 8. It is called projective if there are no duplicate columns in the generator matrix. The possible lengths of 8-divisible linear block codes have been classified except for length n=59, where it is undecided whether such a linear code exists. The possible dimensions satisfy \\(10 \\le k \\le 20\\). Instance 8div_n59_kXX contains the corresponding feasibility problem. Projective binary 8-divisible linear block codes occur as hole configurations of so-called partial solid spreads in finite geometry. Binary 4-divisible linear block codes have applications in physics. | 0.258802 | 2 | |
| prod1 [MIPLIB] | MIPLIB submission pool | Imported from the MIPLIB2010 submissions. | 0.653025 | 3 | |
| fhnw-schedule-pairb400 [MIPLIB] | Simon Felix | Continuous-time project scheduling and selection, inspired by an industry use-case. Each project has a value, the sum should be maximized. Each project has a deadline, and an earliest start date. Three formulations of the same problem ("Pair A", "Pair B" and "Slot") - we expect "Pair B" to be the best formulation. | 0.845716 | 4 | |
| fhnw-schedule-pairb200 [MIPLIB] | Simon Felix | Continuous-time project scheduling and selection, inspired by an industry use-case. Each project has a value, the sum should be maximized. Each project has a deadline, and an earliest start date. Three formulations of the same problem ("Pair A", "Pair B" and "Slot") - we expect "Pair B" to be the best formulation. | 0.893544 | 5 | |
| MIPLIB Top 5 | 8div-n59k11 [MIPLIB] | Sascha Kurz | Projective binary 8-divisible linear block codes A linear block code is called 8-divisible if the weights of its codewords are divisible by 8. It is called projective if there are no duplicate columns in the generator matrix. The possible lengths of 8-divisible linear block codes have been classified except for length n=59, where it is undecided whether such a linear code exists. The possible dimensions satisfy \\(10 \\le k \\le 20\\). Instance 8div_n59_kXX contains the corresponding feasibility problem. Projective binary 8-divisible linear block codes occur as hole configurations of so-called partial solid spreads in finite geometry. Binary 4-divisible linear block codes have applications in physics. | 0.258109 | 1 |
| 8div-n59k12 [MIPLIB] | Sascha Kurz | Projective binary 8-divisible linear block codes A linear block code is called 8-divisible if the weights of its codewords are divisible by 8. It is called projective if there are no duplicate columns in the generator matrix. The possible lengths of 8-divisible linear block codes have been classified except for length n=59, where it is undecided whether such a linear code exists. The possible dimensions satisfy \\(10 \\le k \\le 20\\). Instance 8div_n59_kXX contains the corresponding feasibility problem. Projective binary 8-divisible linear block codes occur as hole configurations of so-called partial solid spreads in finite geometry. Binary 4-divisible linear block codes have applications in physics. | 0.258802 | 2 | |
| neos-3045796-mogo [MIPLIB] | Jeff Linderoth | (None provided) | 1.490926 | 379 | |
| brazil3 [MIPLIB] | George Fonseca | Educational timetabling problems from several real schools/universities around the world. These instances were originally expressed in the xhstt file format [1] and formulated as Integer Programming models as described at [2]. | 1.576371 | 496 | |
| neos-952987 [MIPLIB] | NEOS Server Submission | Instance coming from the NEOS Server with unknown application | 1.867290 | 742 |
8div-n59k10: Instance-to-Model Comparison Results
| Model Group Assignment from MIPLIB: | 8div |
| Assigned Model Group Rank/ISS in the MIC: | 1 / 0.347 |
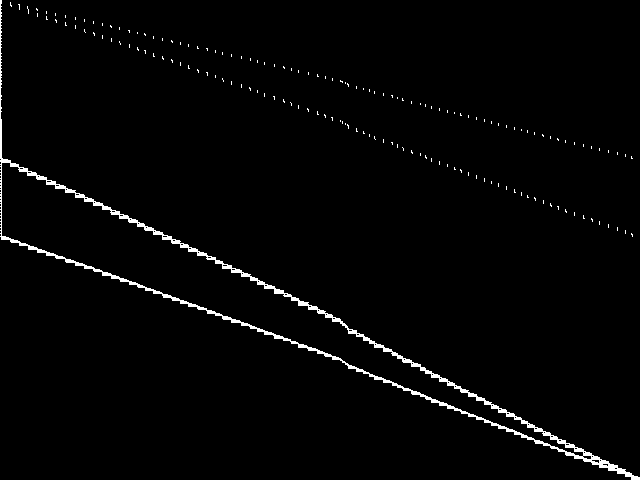
MIC Top 5 Model Groups
These are the 5 model group composite (MGC) images that are most similar to the decomposed CCM image for the query instance, according to the ISS metric.  |
These are model group composite (MGC) images for the MIC top 5 model groups.
|
 |
 |
 |
 |
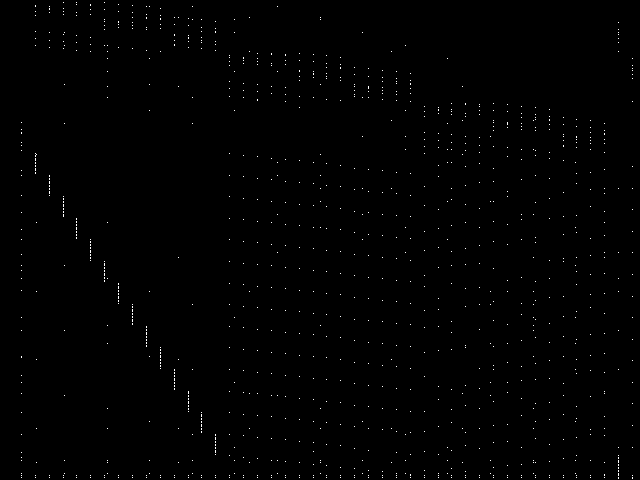 |
| Name | 8div | neos-pseudoapplication-95 | neos-pseudoapplication-74 | scp | stein | |
|
Rank / ISS
The image-based structural similarity (ISS) metric measures the Euclidean distance between the image-based feature vectors for the query instance and all other instances. A smaller ISS value indicates greater similarity.
|
1 / 0.347 | 2 / 1.498 | 3 / 1.554 | 4 / 1.646 | 5 / 1.648 |
Model Group Summary
The table below contains summary information for the five most similar model groups to 8div-n59k10 according to the MIC.
| MODEL GROUP | SUBMITTER | DESCRIPTION | ISS | RANK | |
|---|---|---|---|---|---|
| MIC Top 5 | 8div | Sascha Kurz | Projective binary 8-divisible linear block codes A linear block code is called 8-divisible if the weights of its codewords are divisible by 8. It is called projective if there are no duplicate columns in the generator matrix. The possible lengths of 8-divisible linear block codes have been classified except for length n=59, where it is undecided whether such a linear code exists. The possible dimensions satisfy \\(10 \\le k \\le 20\\). Model 8div_n59_kXX contains the corresponding feasibility problem. Projective binary 8-divisible linear block codes occur as hole configurations of so-called partial solid spreads in finite geometry. Binary 4-divisible linear block codes have applications in physics. | 0.347012 | 1 |
| neos-pseudoapplication-95 | NEOS Server Submission | Imported from the MIPLIB2010 submissions. | 1.498374 | 2 | |
| neos-pseudoapplication-74 | Jeff Linderoth | (None provided) | 1.553987 | 3 | |
| scp | Shunji Umetani | This is a random test model generator for SCP using the scheme of the following paper, namely the column cost c[j] are integer randomly generated from [1,100]; every column covers at least one row; and every row is covered by at least two columns. see reference: E. Balas and A. Ho, Set covering algorithms using cutting planes, heuristics, and subgradient optimization: A computational study, Mathematical Programming, 12 (1980), 37-60. We have newly generated Classes I-N with the following parameter values, where each class has five models. We have also generated reduced models by a standard pricing method in the following paper: S. Umetani and M. Yagiura, Relaxation heuristics for the set covering problem, Journal of the Operations Research Society of Japan, 50 (2007), 350-375. You can obtain the model generator program from the following web site. https://sites.google.com/site/shunjiumetani/benchmark | 1.646027 | 4 | |
| stein | MIPLIB submission pool | Imported from the MIPLIB2010 submissions. | 1.648113 | 5 |

