×
![]()
prod1: Instance-to-Instance Comparison Results
| Type: | Instance |
| Submitter: | MIPLIB submission pool |
| Description: | Imported from the MIPLIB2010 submissions. |
| MIPLIB Entry |
Parent Instance (prod1)
All other instances below were be compared against this "query" instance.  |
 |
 |
 |
 |
 |
|
Raw
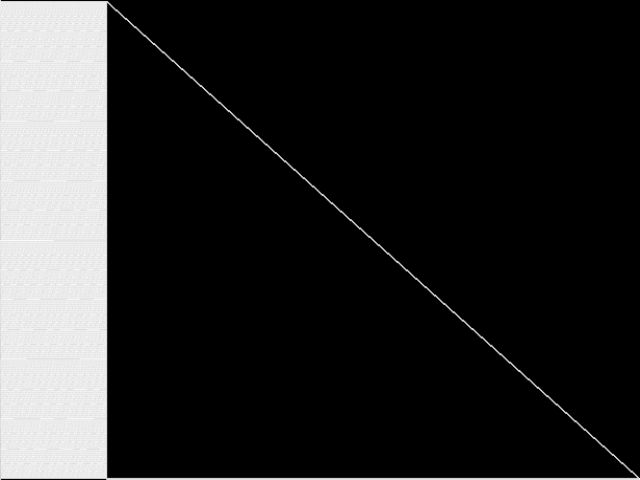
This is the CCM image before the decomposition procedure has been applied.
|
Decomposed
This is the CCM image after a decomposition procedure has been applied. This is the image used by the MIC's image-based comparisons for this query instance.
|
Composite of MIC Top 5
Composite of the five decomposed CCM images from the MIC Top 5.
|
Composite of MIPLIB Top 5
Composite of the five decomposed CCM images from the MIPLIB Top 5.
|
Model Group Composite Image
Composite of the decomposed CCM images for every instance in the same model group as this query.
|
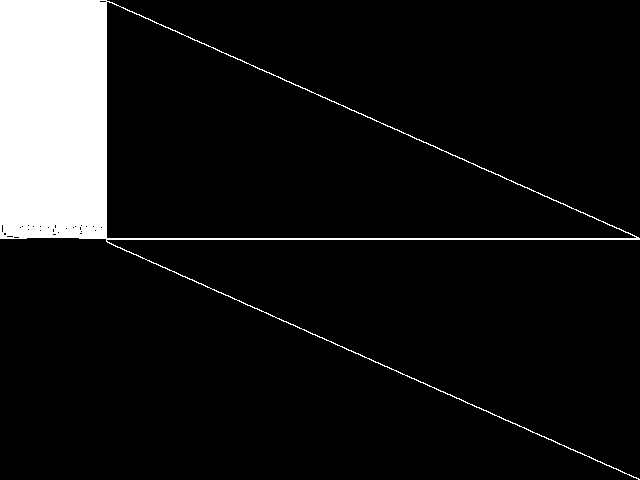
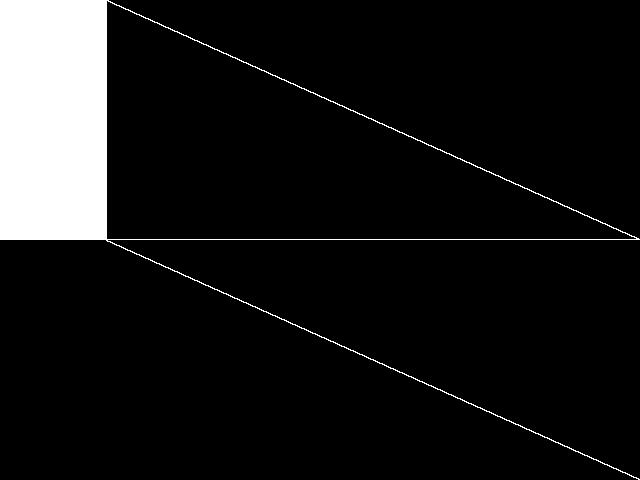
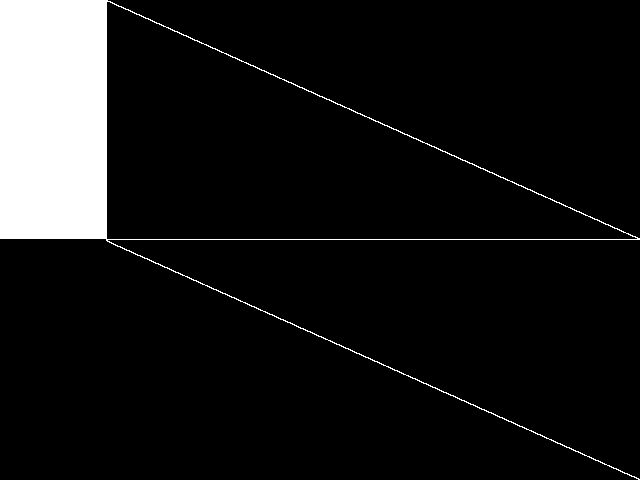
MIC Top 5 Instances
These are the 5 decomposed CCM images that are most similar to decomposed CCM image for the the query instance, according to the ISS metric.  |
Decomposed
These decomposed images were created by GCG.
|
 |
 |
 |
 |
 |
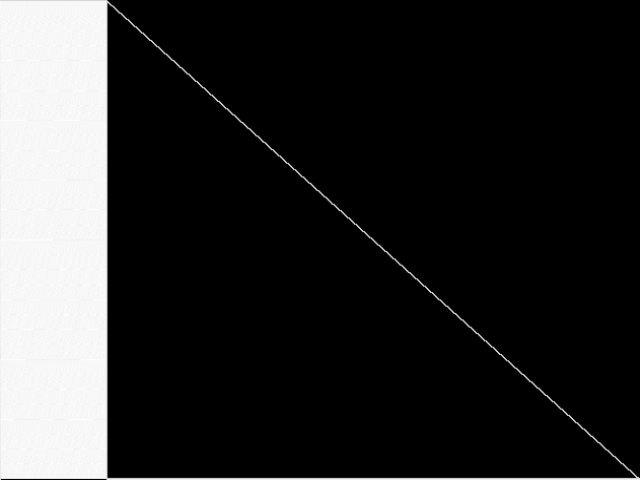
| Name | 8div-n59k10 [MIPLIB] | 8div-n59k12 [MIPLIB] | 8div-n59k11 [MIPLIB] | prod2 [MIPLIB] | gt2 [MIPLIB] | |
|
Rank / ISS
The image-based structural similarity (ISS) metric measures the Euclidean distance between the image-based feature vectors for the query instance and all other instances. A smaller ISS value indicates greater similarity.
|
1 / 0.653 | 2 / 0.658 | 3 / 0.663 | 4 / 0.754 | 5 / 0.760 | |
|
Raw
These images represent the CCM images in their raw forms (before any decomposition was applied) for the MIC top 5.
|
 |
 |
 |
 |
 |
MIPLIB Top 5 Instances
These are the 5 instances that are most closely related to the query instance, according to the instance statistic-based similarity measure employed by MIPLIB 2017  |
Decomposed
These decomposed images were created by GCG.
|
 |
 |
 |
 |
 |
| Name | prod2 [MIPLIB] | neos-1430701 [MIPLIB] | neos-1442119 [MIPLIB] | ns1208400 [MIPLIB] | neos-1171448 [MIPLIB] | |
|
Rank / ISS
The image-based structural similarity (ISS) metric measures the Euclidean distance between the image-based feature vectors for the query instance and all model groups. A smaller ISS value indicates greater similarity.
|
4 / 0.754 | 76 / 1.093 | 564 / 1.535 | 763 / 1.858 | 961 / 3.153 | |
|
Raw
These images represent the CCM images in their raw forms (before any decomposition was applied) for the MIPLIB top 5.
|
 |
 |
 |
 |
 |
Instance Summary
The table below contains summary information for prod1, the five most similar instances to prod1 according to the MIC, and the five most similar instances to prod1 according to MIPLIB 2017.
| INSTANCE | SUBMITTER | DESCRIPTION | ISS | RANK | |
|---|---|---|---|---|---|
| Parent Instance | prod1 [MIPLIB] | MIPLIB submission pool | Imported from the MIPLIB2010 submissions. | 0.000000 | - |
| MIC Top 5 | 8div-n59k10 [MIPLIB] | Sascha Kurz | Projective binary 8-divisible linear block codes A linear block code is called 8-divisible if the weights of its codewords are divisible by 8. It is called projective if there are no duplicate columns in the generator matrix. The possible lengths of 8-divisible linear block codes have been classified except for length n=59, where it is undecided whether such a linear code exists. The possible dimensions satisfy \\(10 \\le k \\le 20\\). Instance 8div_n59_kXX contains the corresponding feasibility problem. Projective binary 8-divisible linear block codes occur as hole configurations of so-called partial solid spreads in finite geometry. Binary 4-divisible linear block codes have applications in physics. | 0.653025 | 1 |
| 8div-n59k12 [MIPLIB] | Sascha Kurz | Projective binary 8-divisible linear block codes A linear block code is called 8-divisible if the weights of its codewords are divisible by 8. It is called projective if there are no duplicate columns in the generator matrix. The possible lengths of 8-divisible linear block codes have been classified except for length n=59, where it is undecided whether such a linear code exists. The possible dimensions satisfy \\(10 \\le k \\le 20\\). Instance 8div_n59_kXX contains the corresponding feasibility problem. Projective binary 8-divisible linear block codes occur as hole configurations of so-called partial solid spreads in finite geometry. Binary 4-divisible linear block codes have applications in physics. | 0.658315 | 2 | |
| 8div-n59k11 [MIPLIB] | Sascha Kurz | Projective binary 8-divisible linear block codes A linear block code is called 8-divisible if the weights of its codewords are divisible by 8. It is called projective if there are no duplicate columns in the generator matrix. The possible lengths of 8-divisible linear block codes have been classified except for length n=59, where it is undecided whether such a linear code exists. The possible dimensions satisfy \\(10 \\le k \\le 20\\). Instance 8div_n59_kXX contains the corresponding feasibility problem. Projective binary 8-divisible linear block codes occur as hole configurations of so-called partial solid spreads in finite geometry. Binary 4-divisible linear block codes have applications in physics. | 0.662822 | 3 | |
| prod2 [MIPLIB] | MIPLIB submission pool | Imported from the MIPLIB2010 submissions. | 0.754176 | 4 | |
| gt2 [MIPLIB] | MIPLIB submission pool | Imported from the MIPLIB2010 submissions. | 0.759981 | 5 | |
| MIPLIB Top 5 | prod2 [MIPLIB] | MIPLIB submission pool | Imported from the MIPLIB2010 submissions. | 0.754176 | 4 |
| neos-1430701 [MIPLIB] | NEOS Server Submission | Imported from the MIPLIB2010 submissions. | 1.092954 | 76 | |
| neos-1442119 [MIPLIB] | NEOS Server Submission | Instance coming from the NEOS Server with unknown application | 1.534657 | 564 | |
| ns1208400 [MIPLIB] | NEOS Server Submission | Instance coming from the NEOS Server with unknown application | 1.858146 | 763 | |
| neos-1171448 [MIPLIB] | NEOS Server Submission | Imported from the MIPLIB2010 submissions. | 3.152592 | 961 |
prod1: Instance-to-Model Comparison Results
| Model Group Assignment from MIPLIB: | no model group assignment |
| Assigned Model Group Rank/ISS in the MIC: | N.A. / N.A. |
MIC Top 5 Model Groups
These are the 5 model group composite (MGC) images that are most similar to the decomposed CCM image for the query instance, according to the ISS metric.  |
These are model group composite (MGC) images for the MIC top 5 model groups.
|
 |
 |
 |
 |
 |
| Name | neos-pseudoapplication-74 | 8div | hypothyroid | bnatt | scp | |
|
Rank / ISS
The image-based structural similarity (ISS) metric measures the Euclidean distance between the image-based feature vectors for the query instance and all other instances. A smaller ISS value indicates greater similarity.
|
1 / 1.447 | 2 / 1.493 | 3 / 1.522 | 4 / 1.622 | 5 / 1.638 |
Model Group Summary
The table below contains summary information for the five most similar model groups to prod1 according to the MIC.
| MODEL GROUP | SUBMITTER | DESCRIPTION | ISS | RANK | |
|---|---|---|---|---|---|
| MIC Top 5 | neos-pseudoapplication-74 | Jeff Linderoth | (None provided) | 1.446882 | 1 |
| 8div | Sascha Kurz | Projective binary 8-divisible linear block codes A linear block code is called 8-divisible if the weights of its codewords are divisible by 8. It is called projective if there are no duplicate columns in the generator matrix. The possible lengths of 8-divisible linear block codes have been classified except for length n=59, where it is undecided whether such a linear code exists. The possible dimensions satisfy \\(10 \\le k \\le 20\\). Model 8div_n59_kXX contains the corresponding feasibility problem. Projective binary 8-divisible linear block codes occur as hole configurations of so-called partial solid spreads in finite geometry. Binary 4-divisible linear block codes have applications in physics. | 1.493220 | 2 | |
| hypothyroid | Gleb Belov | Linearized Constraint Programming models of the MiniZinc Challenges 2012-2016. I should be able to produce versions with indicator constraints supported by Gurobi and CPLEX, however don't know if you can use them and if there is a standard format. These MPS were produced by Gurobi 7.0.2 using the MiniZinc develop branch on eb536656062ca13325a96b5d0881742c7d0e3c38 | 1.521888 | 3 | |
| bnatt | Tatsuya Akutsu | We are submitting ILP data for identification of a singletonattractor in a Boolean newtork, which is a well-known problemin computational systems biology.This problem is known to be NP-hard and we developed a methodto transform an model of the problem to an integer linearprogram (ILP).We used ILPs from artificially generated Boolean networks ofindegree 3.The size of the networks are: 350, 400, 500.Even for the case of 500, we could not find a solution within6 hours using CPLEX 11.2 on a PC with XEON 5470 3.33GHz CPU.(This ILP corresponds to the case of size=350.File format is (zipped) CPLEX LP format.)The details of the method appeared in:T. Akutsu, M. Hayashida and T. Tamura, Integer programming-basedmethods for attractor detection and control of Boolean networks,Proc. The combined 48th IEEE Conference on Decision and Controland 28th Chinese Control Conference (IEEE CDC/CCC 2009), 5610-5617, 2009. | 1.622448 | 4 | |
| scp | Shunji Umetani | This is a random test model generator for SCP using the scheme of the following paper, namely the column cost c[j] are integer randomly generated from [1,100]; every column covers at least one row; and every row is covered by at least two columns. see reference: E. Balas and A. Ho, Set covering algorithms using cutting planes, heuristics, and subgradient optimization: A computational study, Mathematical Programming, 12 (1980), 37-60. We have newly generated Classes I-N with the following parameter values, where each class has five models. We have also generated reduced models by a standard pricing method in the following paper: S. Umetani and M. Yagiura, Relaxation heuristics for the set covering problem, Journal of the Operations Research Society of Japan, 50 (2007), 350-375. You can obtain the model generator program from the following web site. https://sites.google.com/site/shunjiumetani/benchmark | 1.637504 | 5 |

