Instance - bppc6-02

bppc6-02: Instance-to-Instance Comparison Results

Type:	Instance
Submitter:	Manuel Iori
Description:	The models that we attach solve the "bar-relaxation", also known as the "Bin Packing Problem with Contiguity" or the "P\|\|Cmax with contiguity". This is one of the most interesting relaxations for two dimensional cutting and packing problems. Its solution by means of an ILP software is the bottleneck of the primal decomposition methods that we attempted in the paper cited below. In detail, the files correspond to model (12)-(15) in the paper, applied to the instances of the Classes 4, 6 and 8 by Martello and Vigo (Management Science, 1998).
	MIPLIB Entry


	Raw This is the CCM image before the decomposition procedure has been applied.	Decomposed This is the CCM image after a decomposition procedure has been applied. This is the image used by the MIC's image-based comparisons for this query instance.	Composite of MIC Top 5 Composite of the five decomposed CCM images from the MIC Top 5.	Composite of MIPLIB Top 5 Composite of the five decomposed CCM images from the MIPLIB Top 5.	Model Group Composite Image Composite of the decomposed CCM images for every instance in the same model group as this query.

Decomposed These decomposed images were created by GCG.
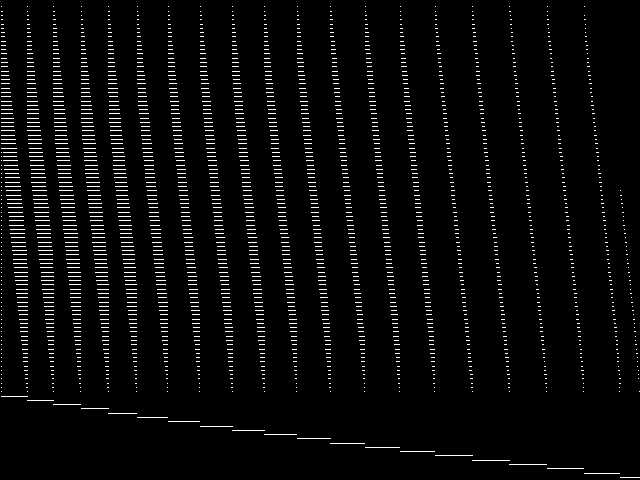Name	bppc6-06 [MIPLIB]	bppc4-08 [MIPLIB]	air05 [MIPLIB]	air04 [MIPLIB]	dolom1 [MIPLIB]
Rank / ISS The image-based structural similarity (ISS) metric measures the Euclidean distance between the image-based feature vectors for the query instance and all other instances. A smaller ISS value indicates greater similarity.	1 / 1.064	2 / 1.270	3 / 1.482	4 / 1.519	5 / 1.533
Raw These images represent the CCM images in their raw forms (before any decomposition was applied) for the MIC top 5.

Decomposed These decomposed images were created by GCG.
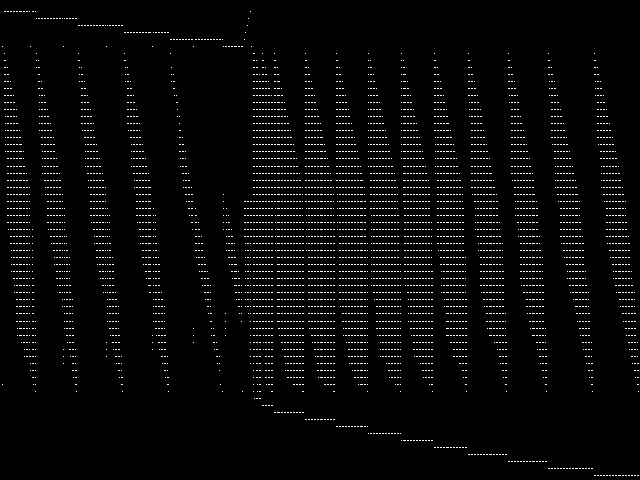Name	bppc6-06 [MIPLIB]	bppc4-08 [MIPLIB]	assign1-10-4 [MIPLIB]	bppc8-09 [MIPLIB]	assign1-5-8 [MIPLIB]
Rank / ISS The image-based structural similarity (ISS) metric measures the Euclidean distance between the image-based feature vectors for the query instance and all model groups. A smaller ISS value indicates greater similarity.	1 / 1.064	2 / 1.270	47 / 1.965	63 / 2.085	170 / 2.830
Raw These images represent the CCM images in their raw forms (before any decomposition was applied) for the MIPLIB top 5.

Instance Summary

The table below contains summary information for bppc6-02, the five most similar instances to bppc6-02 according to the MIC, and the five most similar instances to bppc6-02 according to MIPLIB 2017.

	INSTANCE	SUBMITTER	DESCRIPTION	ISS	RANK
Parent Instance	bppc6-02 [MIPLIB]	Manuel Iori	The models that we attach solve the "bar-relaxation", also known as the "Bin Packing Problem with Contiguity" or the "P\|\|Cmax with contiguity". This is one of the most interesting relaxations for two dimensional cutting and packing problems. Its solution by means of an ILP software is the bottleneck of the primal decomposition methods that we attempted in the paper cited below. In detail, the files correspond to model (12)-(15) in the paper, applied to the instances of the Classes 4, 6 and 8 by Martello and Vigo (Management Science, 1998).	0.000000	-
MIC Top 5	bppc6-06 [MIPLIB]	Manuel Iori	The models that we attach solve the "bar-relaxation", also known as the "Bin Packing Problem with Contiguity" or the "P\|\|Cmax with contiguity". This is one of the most interesting relaxations for two dimensional cutting and packing problems. Its solution by means of an ILP software is the bottleneck of the primal decomposition methods that we attempted in the paper cited below. In detail, the files correspond to model (12)-(15) in the paper, applied to the instances of the Classes 4, 6 and 8 by Martello and Vigo (Management Science, 1998).	1.063780	1
	bppc4-08 [MIPLIB]	Manuel Iori	The models that we attach solve the "bar-relaxation", also known as the "Bin Packing Problem with Contiguity" or the "P\|\|Cmax with contiguity". This is one of the most interesting relaxations for two dimensional cutting and packing problems. Its solution by means of an ILP software is the bottleneck of the primal decomposition methods that we attempted in the paper cited below. In detail, the files correspond to model (12)-(15) in the paper, applied to the instances of the Classes 4, 6 and 8 by Martello and Vigo (Management Science, 1998).	1.269849	2
	air05 [MIPLIB]	G. Astfalk	Airline crew scheduling set partitioning problem	1.481971	3
	air04 [MIPLIB]	G. Astfalk	Airline crew scheduling set partitioning problem	1.518626	4
	dolom1 [MIPLIB]	Double-Click SAS	Crew scheduling instance. Solved with ParaSCIP with SCIP 3.0.1 linked to CPLEX 12.5 as an LP solver on HLRN III with 12288 cores in two runs First run found a feasible solution whose objective function value is 6615265.0000. Giving the feasible solution, the second run solved the instance in 13684.7671 sec.	1.533255	5
MIPLIB Top 5	bppc6-06 [MIPLIB]	Manuel Iori	The models that we attach solve the "bar-relaxation", also known as the "Bin Packing Problem with Contiguity" or the "P\|\|Cmax with contiguity". This is one of the most interesting relaxations for two dimensional cutting and packing problems. Its solution by means of an ILP software is the bottleneck of the primal decomposition methods that we attempted in the paper cited below. In detail, the files correspond to model (12)-(15) in the paper, applied to the instances of the Classes 4, 6 and 8 by Martello and Vigo (Management Science, 1998).	1.063780	1
	bppc4-08 [MIPLIB]	Manuel Iori	The models that we attach solve the "bar-relaxation", also known as the "Bin Packing Problem with Contiguity" or the "P\|\|Cmax with contiguity". This is one of the most interesting relaxations for two dimensional cutting and packing problems. Its solution by means of an ILP software is the bottleneck of the primal decomposition methods that we attempted in the paper cited below. In detail, the files correspond to model (12)-(15) in the paper, applied to the instances of the Classes 4, 6 and 8 by Martello and Vigo (Management Science, 1998).	1.269849	2
	assign1-10-4 [MIPLIB]	Robert Fourer	Imported from the MIPLIB2010 submissions.	1.964628	47
	bppc8-09 [MIPLIB]	Manuel Iori	The models that we attach solve the "bar-relaxation", also known as the "Bin Packing Problem with Contiguity" or the "P\|\|Cmax with contiguity". This is one of the most interesting relaxations for two dimensional cutting and packing problems. Its solution by means of an ILP software is the bottleneck of the primal decomposition methods that we attempted in the paper cited below. In detail, the files correspond to model (12)-(15) in the paper, applied to the instances of the Classes 4, 6 and 8 by Martello and Vigo (Management Science, 1998).	2.085360	63
	assign1-5-8 [MIPLIB]	Robert Fourer	Imported from the MIPLIB2010 submissions.	2.830397	170

bppc6-02: Instance-to-Model Comparison Results

Model Group Assignment from MIPLIB:	bppc
Assigned Model Group Rank/ISS in the MIC:	1 / 1.504

These are model group composite (MGC) images for the MIC top 5 model groups.
Name	bppc	neos-pseudoapplication-103	selofsubspaces	neos-pseudoapplication-23	2hopcds
Rank / ISS The image-based structural similarity (ISS) metric measures the Euclidean distance between the image-based feature vectors for the query instance and all other instances. A smaller ISS value indicates greater similarity.	1 / 1.504	2 / 1.905	3 / 1.926	4 / 1.934	5 / 1.946

Model Group Summary

The table below contains summary information for the five most similar model groups to bppc6-02 according to the MIC.

	MODEL GROUP	SUBMITTER	DESCRIPTION	ISS	RANK
MIC Top 5	bppc	Manuel Iori	The models that we attach solve the "bar-relaxation", also known as the "Bin Packing Problem with Contiguity" or the "P\|\|Cmax with contiguity". This is one of the most interesting relaxations for two dimensional cutting and packing problems. Its solution by means of an ILP software is the bottleneck of the primal decomposition methods that we attempted in the paper cited below. In detail, the files correspond to model (12)-(15) in the paper, applied to the models of the Classes 4, 6 and 8 by Martello and Vigo (Management Science, 1998).	1.504261	1
	neos-pseudoapplication-103	Hans Mittelmann	Collection of anonymous submissions to the NEOS Server for Optimization	1.904611	2
	selofsubspaces	Daniel Heinlein	Clique problems arising from a selection problem of subspaces in the PG(7,2) with different prescribed variables and numerically instable linear programming relaxation.	1.926267	3
	neos-pseudoapplication-23	NEOS Server Submission	Imported from the MIPLIB2010 submissions.	1.933629	4
	2hopcds	Austin Buchanan	A problem in wireless networks. The objective is to select a minimum number of relay nodes so that any two nonadjacent nodes can communicate by way of the chosen relay nodes in at most s hops, where s is a problem input. The 2-hop case of this problem can be formulated as a set cover/hitting set problem with n binary variables and n^2 constraints: _{ k N(i) N(j) } x_k 1 for nonadjacent node pairs {i,j}. Despite the formulation's simplicity, models with as few as 120 variables are left unsolved after one hour using Gurobi 7.0.2.	1.945573	5

bppc6-02: Instance-to-Instance Comparison Results

Parent Instance (bppc6-02)

MIC Top 5 Instances

MIPLIB Top 5 Instances

Instance Summary

bppc6-02: Instance-to-Model Comparison Results

MIC Top 5 Model Groups

Model Group Summary