×
![]()
bppc
| Type: | Model Group |
| Submitter: | Manuel Iori |
| Description: | The models that we attach solve the "bar-relaxation", also known as the "Bin Packing Problem with Contiguity" or the "P||Cmax with contiguity". This is one of the most interesting relaxations for two dimensional cutting and packing problems. Its solution by means of an ILP software is the bottleneck of the primal decomposition methods that we attempted in the paper cited below. In detail, the files correspond to model (12)-(15) in the paper, applied to the models of the Classes 4, 6 and 8 by Martello and Vigo (Management Science, 1998). |
Parent Model Group (bppc)
All other model groups below were be compared against this "query" model group.  |
 |
|
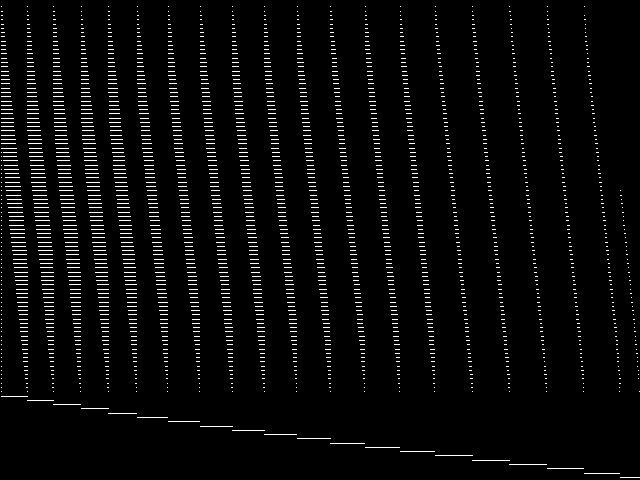
Model Group Composite (MGC) image
Composite of the decomposed CCM images for every instance in the query model group.
|
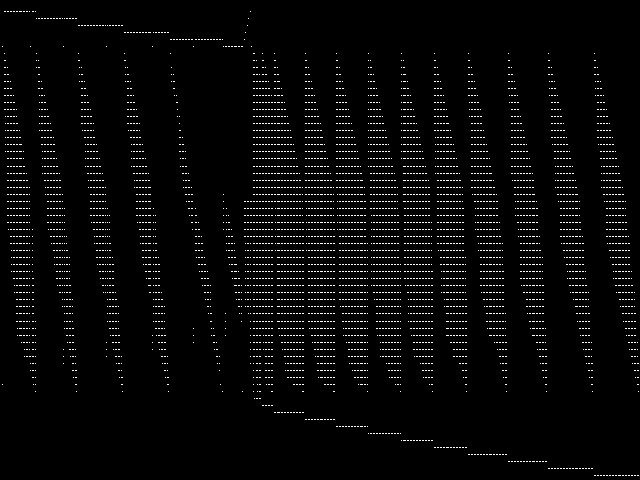
Component Instances (Decomposed)
These are the decomposed CCM images for each instance in the query model group.MIC Top 5 Model Groups
These are the 5 MGC images that are most similar to the MGC image for the query model group, according to the ISS metric.  |
FIXME - These are model group composite images.
|
 |
 |
 |
 |
 |
| Name | reblock | neos-pseudoapplication-46 | neos-pseudoapplication-23 | iis | neos-pseudoapplication-106 | |
|
Rank / ISS
The image-based structural similarity (ISS) metric measures the Euclidean distance between the image-based feature vectors for the query model group and all other model groups. A smaller ISS value indicates greater similarity.
|
1 / 1.501 | 2 / 1.542 | 3 / 1.546 | 4 / 1.571 | 5 / 1.580 |
Model Group Summary
The table below contains summary information for bppc, and for the five most similar model groups to bppc according to the MIC.
| MODEL GROUP | SUBMITTER | DESCRIPTION | ISS | RANK | |
|---|---|---|---|---|---|
| Parent Model Group | bppc | Manuel Iori | The models that we attach solve the "bar-relaxation", also known as the "Bin Packing Problem with Contiguity" or the "P||Cmax with contiguity". This is one of the most interesting relaxations for two dimensional cutting and packing problems. Its solution by means of an ILP software is the bottleneck of the primal decomposition methods that we attempted in the paper cited below. In detail, the files correspond to model (12)-(15) in the paper, applied to the models of the Classes 4, 6 and 8 by Martello and Vigo (Management Science, 1998). | 0.000000 | - |
| MIC Top 5 | reblock | Andreas Bley | Multi-period mine production scheduling model. Solved using ug[SCIP/spx], a distributed massively parallel version of SCIP run on 2,000 cores at the HLRN-II super computer facility. | 1.501099 | 1 |
| neos-pseudoapplication-46 | NEOS Server Submission | Imported from the MIPLIB2010 submissions. | 1.541884 | 2 | |
| neos-pseudoapplication-23 | NEOS Server Submission | Imported from the MIPLIB2010 submissions. | 1.546313 | 3 | |
| iis | Marc Pfetsch | 23 "middlehard" Set-Covering Models for MIPLIB: they have a small number of variables compared to the number of constraints and CPLEX 12.1 needs about one hour to solve them.For more information, have a look into the readme file which explains how the models can be created. | 1.571433 | 4 | |
| neos-pseudoapplication-106 | Hans Mittelmann | Collection of anonymous submissions to the NEOS Server for Optimization | 1.580373 | 5 |