Instance - fastxgemm-n3r23s5t6

fastxgemm-n3r23s5t6: Instance-to-Instance Comparison Results

Type:	Instance
Submitter:	Laurent Sorber
Description:	Naive multiplication of two N by N matrices requires N^3 scalar multiplications. For N=2, Strassen showed that it could be done in only R=7 < 8=N^3 multiplications. For N=3, it is known that 19 <= R <= 23, and for N=4 it is known that 34 <= R <= 49. This repository contains code that generates a mixed-integer linear program (MILP) formulation of the fast matrix multiplication problem for finding solutions with R < N^3 and proving that they are optimal. For a more detailed description, see the accompanying manuscript.
	MIPLIB Entry


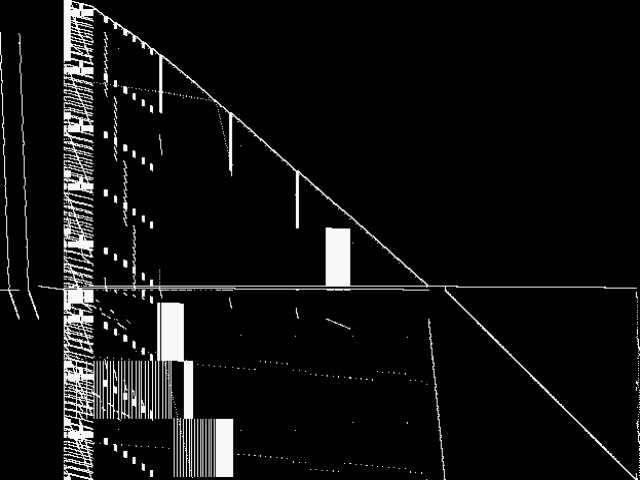
	Raw This is the CCM image before the decomposition procedure has been applied.	Decomposed This is the CCM image after a decomposition procedure has been applied. This is the image used by the MIC's image-based comparisons for this query instance.	Composite of MIC Top 5 Composite of the five decomposed CCM images from the MIC Top 5.	Composite of MIPLIB Top 5 Composite of the five decomposed CCM images from the MIPLIB Top 5.	Model Group Composite Image Composite of the decomposed CCM images for every instance in the same model group as this query.

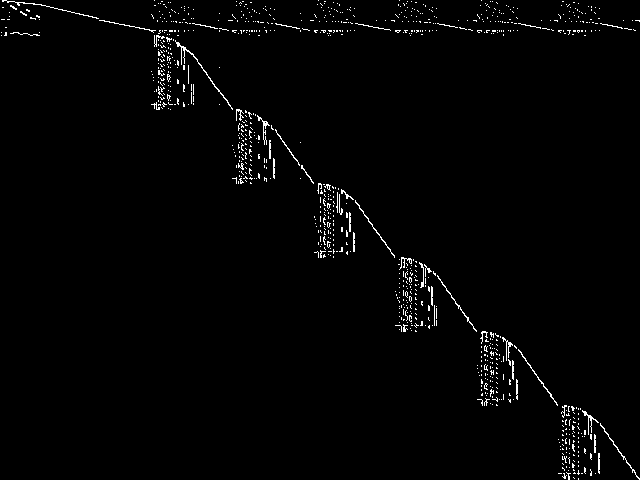
Decomposed These decomposed images were created by GCG.
Name	fastxgemm-n3r22s4t6 [MIPLIB]	fastxgemm-n3r21s3t6 [MIPLIB]	graph20-20-1rand [MIPLIB]	mappingmesh3x3mpeg2i [MIPLIB]	neos-3209519-ruhr [MIPLIB]
Rank / ISS The image-based structural similarity (ISS) metric measures the Euclidean distance between the image-based feature vectors for the query instance and all other instances. A smaller ISS value indicates greater similarity.	1 / 0.369	2 / 0.377	3 / 0.602	4 / 0.628	5 / 0.650
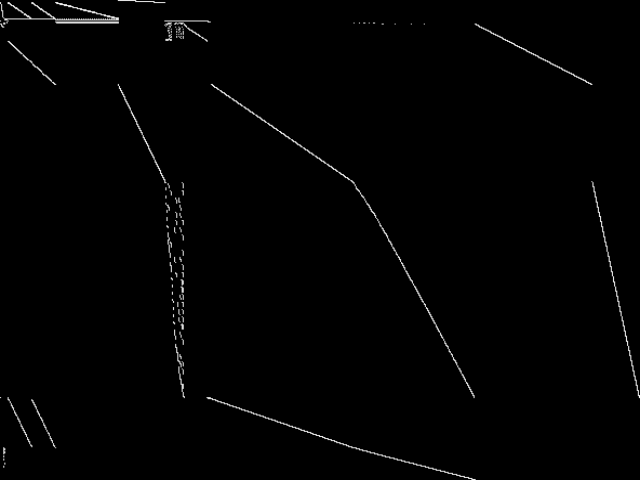
Raw These images represent the CCM images in their raw forms (before any decomposition was applied) for the MIC top 5.

Decomposed These decomposed images were created by GCG.
Name	fastxgemm-n3r22s4t6 [MIPLIB]	fastxgemm-n3r21s3t6 [MIPLIB]	fastxgemm-n2r7s4t1 [MIPLIB]	fastxgemm-n2r6s0t2 [MIPLIB]	neos-4335793-snake [MIPLIB]
Rank / ISS The image-based structural similarity (ISS) metric measures the Euclidean distance between the image-based feature vectors for the query instance and all model groups. A smaller ISS value indicates greater similarity.	1 / 0.369	2 / 0.377	108 / 0.966	112 / 0.978	408 / 1.545
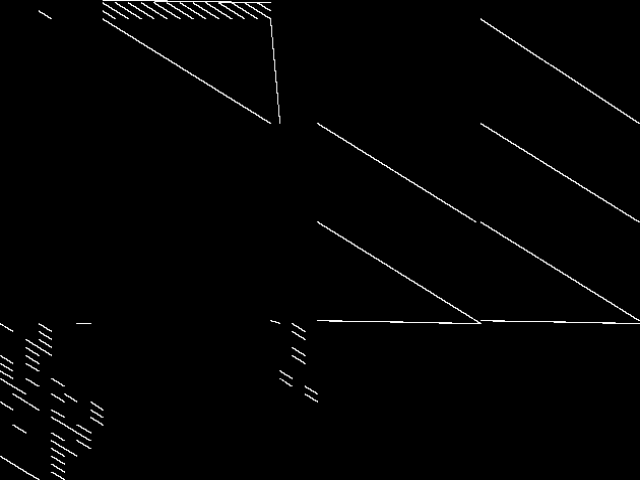
Raw These images represent the CCM images in their raw forms (before any decomposition was applied) for the MIPLIB top 5.

Instance Summary

The table below contains summary information for fastxgemm-n3r23s5t6, the five most similar instances to fastxgemm-n3r23s5t6 according to the MIC, and the five most similar instances to fastxgemm-n3r23s5t6 according to MIPLIB 2017.

	INSTANCE	SUBMITTER	DESCRIPTION	ISS	RANK
Parent Instance	fastxgemm-n3r23s5t6 [MIPLIB]	Laurent Sorber	Naive multiplication of two N by N matrices requires N^3 scalar multiplications. For N=2, Strassen showed that it could be done in only R=7 < 8=N^3 multiplications. For N=3, it is known that 19 <= R <= 23, and for N=4 it is known that 34 <= R <= 49. This repository contains code that generates a mixed-integer linear program (MILP) formulation of the fast matrix multiplication problem for finding solutions with R < N^3 and proving that they are optimal. For a more detailed description, see the accompanying manuscript.	0.000000	-
MIC Top 5	fastxgemm-n3r22s4t6 [MIPLIB]	Laurent Sorber	Naive multiplication of two N by N matrices requires N^3 scalar multiplications. For N=2, Strassen showed that it could be done in only R=7 < 8=N^3 multiplications. For N=3, it is known that 19 <= R <= 23, and for N=4 it is known that 34 <= R <= 49. This repository contains code that generates a mixed-integer linear program (MILP) formulation of the fast matrix multiplication problem for finding solutions with R < N^3 and proving that they are optimal. For a more detailed description, see the accompanying manuscript.	0.369261	1
	fastxgemm-n3r21s3t6 [MIPLIB]	Laurent Sorber	Naive multiplication of two N by N matrices requires N^3 scalar multiplications. For N=2, Strassen showed that it could be done in only R=7 < 8=N^3 multiplications. For N=3, it is known that 19 <= R <= 23, and for N=4 it is known that 34 <= R <= 49. This repository contains code that generates a mixed-integer linear program (MILP) formulation of the fast matrix multiplication problem for finding solutions with R < N^3 and proving that they are optimal. For a more detailed description, see the accompanying manuscript.	0.376725	2
	graph20-20-1rand [MIPLIB]	Michael Bastubbe	Packing Cuts in Undirected Graphs. Instances are described in 4.1.	0.602493	3
	mappingmesh3x3mpeg2i [MIPLIB]	Gleb Belov	These are the instances from MiniZinc Challenges 2012-2016 (see www.minizinc.org), compiled for MIP WITH INDICATOR CONSTRAINTS using the develop branch of MiniZinc and CPLEX 12.7.1 on 30 April 2017. Thus, these instances can only be handled by solvers accepting indicator constraints. For instances compiled with big-M/domain decomposition only, see my previous submission to MIPLIB.To recompile, create a directory MODELS, a list lst12_16.txt of the instances with full paths to mzn/dzn files of each instance per line, and say$> ~/install/libmzn/tests/benchmarking/mzn-test.py -l ../lst12_16.txt -slvPrf MZN-CPLEX -debug 1 -addOption "-timeout 3 -D fIndConstr=true -D fMIPdomains=false" -useJoinedName "-writeModel MODELS_IND/%s.mps" Alternatively, you can compile individual instance as follows: $> mzn-cplex -v -s -G linear -output-time ../challenge_2012_2016/mznc2016_probs/zephyrus/zephyrus.mzn ../challenge_2012_2016/mznc2016_p/zephyrus/14__8__6__3.dzn -a -timeout 3 -D fIndConstr=true -D fMIPdomains=false -writeModel MODELS_IND/challenge_2012_2016mznc2016_probszephyruszephyrusmzn-challenge_2012_2016mznc2016_probszephyrus14__8__6__3dzn.mps	0.628476	4
	neos-3209519-ruhr [MIPLIB]	Jeff Linderoth	(None provided)	0.649904	5
MIPLIB Top 5	fastxgemm-n3r22s4t6 [MIPLIB]	Laurent Sorber	Naive multiplication of two N by N matrices requires N^3 scalar multiplications. For N=2, Strassen showed that it could be done in only R=7 < 8=N^3 multiplications. For N=3, it is known that 19 <= R <= 23, and for N=4 it is known that 34 <= R <= 49. This repository contains code that generates a mixed-integer linear program (MILP) formulation of the fast matrix multiplication problem for finding solutions with R < N^3 and proving that they are optimal. For a more detailed description, see the accompanying manuscript.	0.369261	1
	fastxgemm-n3r21s3t6 [MIPLIB]	Laurent Sorber	Naive multiplication of two N by N matrices requires N^3 scalar multiplications. For N=2, Strassen showed that it could be done in only R=7 < 8=N^3 multiplications. For N=3, it is known that 19 <= R <= 23, and for N=4 it is known that 34 <= R <= 49. This repository contains code that generates a mixed-integer linear program (MILP) formulation of the fast matrix multiplication problem for finding solutions with R < N^3 and proving that they are optimal. For a more detailed description, see the accompanying manuscript.	0.376725	2
	fastxgemm-n2r7s4t1 [MIPLIB]	Laurent Sorber	Naive multiplication of two N by N matrices requires N^3 scalar multiplications. For N=2, Strassen showed that it could be done in only R=7 < 8=N^3 multiplications. For N=3, it is known that 19 <= R <= 23, and for N=4 it is known that 34 <= R <= 49. This repository contains code that generates a mixed-integer linear program (MILP) formulation of the fast matrix multiplication problem for finding solutions with R < N^3 and proving that they are optimal. For a more detailed description, see the accompanying manuscript.	0.966342	108
	fastxgemm-n2r6s0t2 [MIPLIB]	Laurent Sorber	Naive multiplication of two N by N matrices requires N^3 scalar multiplications. For N=2, Strassen showed that it could be done in only R=7 < 8=N^3 multiplications. For N=3, it is known that 19 <= R <= 23, and for N=4 it is known that 34 <= R <= 49. This repository contains code that generates a mixed-integer linear program (MILP) formulation of the fast matrix multiplication problem for finding solutions with R < N^3 and proving that they are optimal. For a more detailed description, see the accompanying manuscript.	0.977585	112
	neos-4335793-snake [MIPLIB]	Jeff Linderoth	(None provided)	1.544504	408

fastxgemm-n3r23s5t6: Instance-to-Model Comparison Results

Model Group Assignment from MIPLIB:	fastxgemm
Assigned Model Group Rank/ISS in the MIC:	20 / 1.535

These are model group composite (MGC) images for the MIC top 5 model groups.
Name	graphs	mapping	seqsolve	radiation	n37
Rank / ISS The image-based structural similarity (ISS) metric measures the Euclidean distance between the image-based feature vectors for the query instance and all other instances. A smaller ISS value indicates greater similarity.	1 / 0.960	2 / 0.978	3 / 0.998	4 / 1.001	5 / 1.037

Model Group Summary

The table below contains summary information for the five most similar model groups to fastxgemm-n3r23s5t6 according to the MIC.

	MODEL GROUP	SUBMITTER	DESCRIPTION	ISS	RANK
MIC Top 5	graphs	Michael Bastubbe	Packing Cuts in Undirected Graphs. Models are described in 4.1.	0.959612	1
	mapping	Gleb Belov	These are the models from MiniZinc Challenges 2012-2016 (see www.minizinc.org), compiled for MIP WITH INDICATOR CONSTRAINTS using the develop branch of MiniZinc and CPLEX 12.7.1 on 30 April 2017. Thus, these models can only be handled by solvers accepting indicator constraints. For models compiled with big-M/domain decomposition only, see my previous submission to MIPLIB.To recompile, create a directory MODELS, a list lst12_16.txt of the models with full paths to mzn/dzn files of each model per line, and say$> ~/install/libmzn/tests/benchmarking/mzn-test.py -l ../lst12_16.txt -slvPrf MZN-CPLEX -debug 1 -addOption "-timeout 3 -D fIndConstr=true -D fMIPdomains=false" -useJoinedName "-writeModel MODELS_IND/%s.mps" Alternatively, you can compile individual model as follows: $> mzn-cplex -v -s -G linear -output-time ../challenge_2012_2016/mznc2016_probs/zephyrus/zephyrus.mzn ../challenge_2012_2016/mznc2016_p/zephyrus/14__8__6__3.dzn -a -timeout 3 -D fIndConstr=true -D fMIPdomains=false -writeModel MODELS_IND/challenge_2012_2016mznc2016_probszephyruszephyrusmzn-challenge_2012_2016mznc2016_probszephyrus14__8__6__3dzn.mps	0.978268	2
	seqsolve	Irv Lustig	The 3 problems in this group (seqsolve1-seqsolve3) represent a hierarchical optimization process, which is derived from a customer problem for assigning people to sites into blocks of time on days of the week. The specialty of this submission is that the best known solution for seqsolveX can be used as a MIP start for seqsolveX+1. For a description of the connections between the problems, please refer to the README.txt contained in the model data for this submission, which also includes MIP start files and a Gurobi log file.	0.998011	3
	radiation	Gleb Belov	Linearized Constraint Programming models of the MiniZinc Challenges 2012-2016. I should be able to produce versions with indicator constraints supported by Gurobi and CPLEX, however don't know if you can use them and if there is a standard format. These MPS were produced by Gurobi 7.0.2 using the MiniZinc develop branch on eb536656062ca13325a96b5d0881742c7d0e3c38	1.000950	4
	n37	J. Aronson	Fixed charge transportation problem	1.037297	5

fastxgemm-n3r23s5t6: Instance-to-Instance Comparison Results

Parent Instance (fastxgemm-n3r23s5t6)

MIC Top 5 Instances

MIPLIB Top 5 Instances

Instance Summary

fastxgemm-n3r23s5t6: Instance-to-Model Comparison Results

MIC Top 5 Model Groups

Model Group Summary