×
![]()
fastxgemm-n2r6s0t2: Instance-to-Instance Comparison Results
| Type: | Instance |
| Submitter: | Laurent Sorber |
| Description: | Naive multiplication of two N by N matrices requires N^3 scalar multiplications. For N=2, Strassen showed that it could be done in only R=7 < 8=N^3 multiplications. For N=3, it is known that 19 <= R <= 23, and for N=4 it is known that 34 <= R <= 49. This repository contains code that generates a mixed-integer linear program (MILP) formulation of the fast matrix multiplication problem for finding solutions with R < N^3 and proving that they are optimal. For a more detailed description, see the accompanying manuscript. |
| MIPLIB Entry |
Parent Instance (fastxgemm-n2r6s0t2)
All other instances below were be compared against this "query" instance.  |
 |
 |
 |
 |
 |
|
Raw
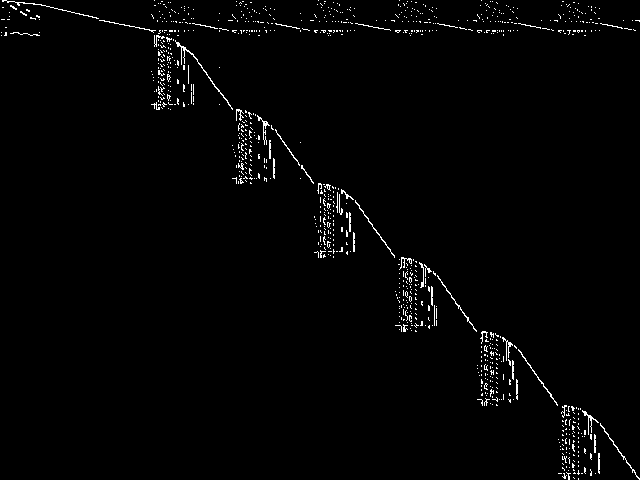
This is the CCM image before the decomposition procedure has been applied.
|
Decomposed
This is the CCM image after a decomposition procedure has been applied. This is the image used by the MIC's image-based comparisons for this query instance.
|
Composite of MIC Top 5
Composite of the five decomposed CCM images from the MIC Top 5.
|
Composite of MIPLIB Top 5
Composite of the five decomposed CCM images from the MIPLIB Top 5.
|
Model Group Composite Image
Composite of the decomposed CCM images for every instance in the same model group as this query.
|
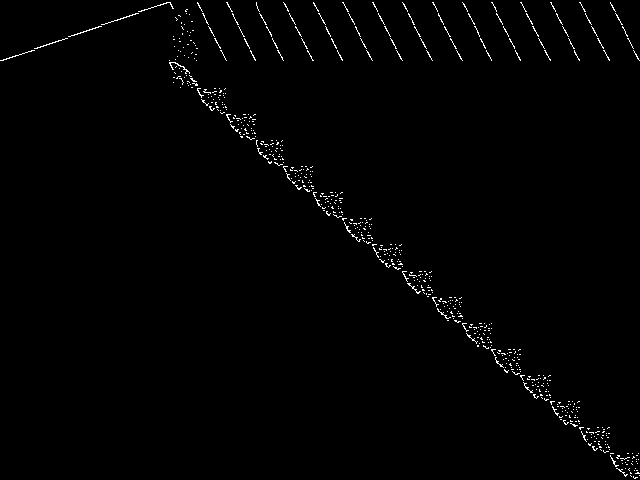
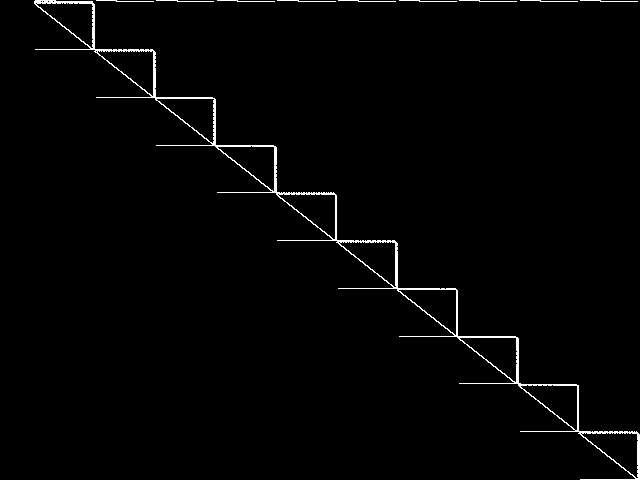
MIC Top 5 Instances
These are the 5 decomposed CCM images that are most similar to decomposed CCM image for the the query instance, according to the ISS metric.  |
Decomposed
These decomposed images were created by GCG.
|
 |
 |
 |
 |
 |
| Name | fastxgemm-n2r7s4t1 [MIPLIB] | ta1-UUM [MIPLIB] | umts [MIPLIB] | neos-5260764-orauea [MIPLIB] | neos-3615091-sutlej [MIPLIB] | |
|
Rank / ISS
The image-based structural similarity (ISS) metric measures the Euclidean distance between the image-based feature vectors for the query instance and all other instances. A smaller ISS value indicates greater similarity.
|
1 / 0.583 | 2 / 0.757 | 3 / 0.869 | 4 / 0.932 | 5 / 0.940 | |
|
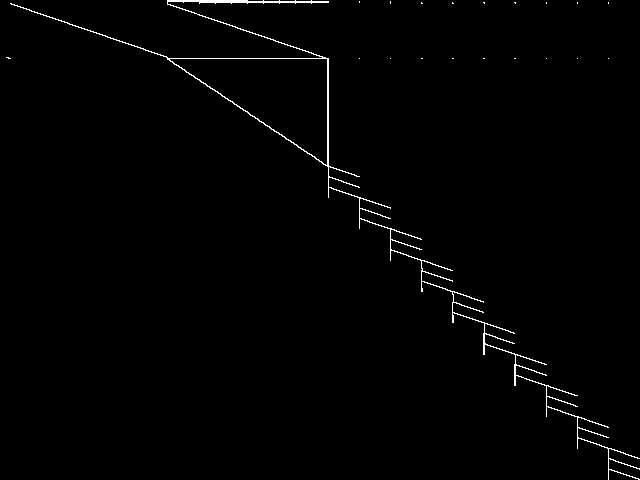
Raw
These images represent the CCM images in their raw forms (before any decomposition was applied) for the MIC top 5.
|
 |
 |
 |
 |
 |
MIPLIB Top 5 Instances
These are the 5 instances that are most closely related to the query instance, according to the instance statistic-based similarity measure employed by MIPLIB 2017  |
Decomposed
These decomposed images were created by GCG.
|
 |
 |
 |
 |
 |
| Name | fastxgemm-n2r7s4t1 [MIPLIB] | fastxgemm-n3r22s4t6 [MIPLIB] | fastxgemm-n3r21s3t6 [MIPLIB] | fastxgemm-n3r23s5t6 [MIPLIB] | neos-4335793-snake [MIPLIB] | |
|
Rank / ISS
The image-based structural similarity (ISS) metric measures the Euclidean distance between the image-based feature vectors for the query instance and all model groups. A smaller ISS value indicates greater similarity.
|
1 / 0.583 | 6 / 0.952 | 10 / 0.968 | 12 / 0.978 | 512 / 1.588 | |
|
Raw
These images represent the CCM images in their raw forms (before any decomposition was applied) for the MIPLIB top 5.
|
 |
 |
 |
 |
 |
Instance Summary
The table below contains summary information for fastxgemm-n2r6s0t2, the five most similar instances to fastxgemm-n2r6s0t2 according to the MIC, and the five most similar instances to fastxgemm-n2r6s0t2 according to MIPLIB 2017.
| INSTANCE | SUBMITTER | DESCRIPTION | ISS | RANK | |
|---|---|---|---|---|---|
| Parent Instance | fastxgemm-n2r6s0t2 [MIPLIB] | Laurent Sorber | Naive multiplication of two N by N matrices requires N^3 scalar multiplications. For N=2, Strassen showed that it could be done in only R=7 < 8=N^3 multiplications. For N=3, it is known that 19 <= R <= 23, and for N=4 it is known that 34 <= R <= 49. This repository contains code that generates a mixed-integer linear program (MILP) formulation of the fast matrix multiplication problem for finding solutions with R < N^3 and proving that they are optimal. For a more detailed description, see the accompanying manuscript. | 0.000000 | - |
| MIC Top 5 | fastxgemm-n2r7s4t1 [MIPLIB] | Laurent Sorber | Naive multiplication of two N by N matrices requires N^3 scalar multiplications. For N=2, Strassen showed that it could be done in only R=7 < 8=N^3 multiplications. For N=3, it is known that 19 <= R <= 23, and for N=4 it is known that 34 <= R <= 49. This repository contains code that generates a mixed-integer linear program (MILP) formulation of the fast matrix multiplication problem for finding solutions with R < N^3 and proving that they are optimal. For a more detailed description, see the accompanying manuscript. | 0.582596 | 1 |
| ta1-UUM [MIPLIB] | MIPLIB submission pool | Imported from the MIPLIB2010 submissions. | 0.756554 | 2 | |
| umts [MIPLIB] | C. Polo | Telecommunications network model | 0.869278 | 3 | |
| neos-5260764-orauea [MIPLIB] | Hans Mittelmann | Seem to be VRP output from 2-hour runs of Gurobi on 12 threads is included | 0.932016 | 4 | |
| neos-3615091-sutlej [MIPLIB] | Hans Mittelmann | Collection of anonymous submissions to the NEOS Server for Optimization | 0.940315 | 5 | |
| MIPLIB Top 5 | fastxgemm-n2r7s4t1 [MIPLIB] | Laurent Sorber | Naive multiplication of two N by N matrices requires N^3 scalar multiplications. For N=2, Strassen showed that it could be done in only R=7 < 8=N^3 multiplications. For N=3, it is known that 19 <= R <= 23, and for N=4 it is known that 34 <= R <= 49. This repository contains code that generates a mixed-integer linear program (MILP) formulation of the fast matrix multiplication problem for finding solutions with R < N^3 and proving that they are optimal. For a more detailed description, see the accompanying manuscript. | 0.582596 | 1 |
| fastxgemm-n3r22s4t6 [MIPLIB] | Laurent Sorber | Naive multiplication of two N by N matrices requires N^3 scalar multiplications. For N=2, Strassen showed that it could be done in only R=7 < 8=N^3 multiplications. For N=3, it is known that 19 <= R <= 23, and for N=4 it is known that 34 <= R <= 49. This repository contains code that generates a mixed-integer linear program (MILP) formulation of the fast matrix multiplication problem for finding solutions with R < N^3 and proving that they are optimal. For a more detailed description, see the accompanying manuscript. | 0.951961 | 6 | |
| fastxgemm-n3r21s3t6 [MIPLIB] | Laurent Sorber | Naive multiplication of two N by N matrices requires N^3 scalar multiplications. For N=2, Strassen showed that it could be done in only R=7 < 8=N^3 multiplications. For N=3, it is known that 19 <= R <= 23, and for N=4 it is known that 34 <= R <= 49. This repository contains code that generates a mixed-integer linear program (MILP) formulation of the fast matrix multiplication problem for finding solutions with R < N^3 and proving that they are optimal. For a more detailed description, see the accompanying manuscript. | 0.967526 | 10 | |
| fastxgemm-n3r23s5t6 [MIPLIB] | Laurent Sorber | Naive multiplication of two N by N matrices requires N^3 scalar multiplications. For N=2, Strassen showed that it could be done in only R=7 < 8=N^3 multiplications. For N=3, it is known that 19 <= R <= 23, and for N=4 it is known that 34 <= R <= 49. This repository contains code that generates a mixed-integer linear program (MILP) formulation of the fast matrix multiplication problem for finding solutions with R < N^3 and proving that they are optimal. For a more detailed description, see the accompanying manuscript. | 0.977585 | 12 | |
| neos-4335793-snake [MIPLIB] | Jeff Linderoth | (None provided) | 1.587881 | 512 |
fastxgemm-n2r6s0t2: Instance-to-Model Comparison Results
| Model Group Assignment from MIPLIB: | fastxgemm |
| Assigned Model Group Rank/ISS in the MIC: | 1 / 1.189 |
MIC Top 5 Model Groups
These are the 5 model group composite (MGC) images that are most similar to the decomposed CCM image for the query instance, according to the ISS metric.  |
These are model group composite (MGC) images for the MIC top 5 model groups.
|
 |
 |
 |
 |
 |
| Name | fastxgemm | mapping | allcolor | noip | sp_product | |
|
Rank / ISS
The image-based structural similarity (ISS) metric measures the Euclidean distance between the image-based feature vectors for the query instance and all other instances. A smaller ISS value indicates greater similarity.
|
1 / 1.190 | 2 / 1.425 | 3 / 1.459 | 4 / 1.476 | 5 / 1.519 |
Model Group Summary
The table below contains summary information for the five most similar model groups to fastxgemm-n2r6s0t2 according to the MIC.
| MODEL GROUP | SUBMITTER | DESCRIPTION | ISS | RANK | |
|---|---|---|---|---|---|
| MIC Top 5 | fastxgemm | Laurent Sorber | Naive multiplication of two N by N matrices requires N^3 scalar multiplications. For N=2, Strassen showed that it could be done in only R=7 < 8=N^3 multiplications. For N=3, it is known that 19 <= R <= 23, and for N=4 it is known that 34 <= R <= 49. This repository contains code that generates a mixed-integer linear program (MILP) formulation of the fast matrix multiplication problem for finding solutions with R < N^3 and proving that they are optimal. For a more detailed description, see the accompanying manuscript. | 1.189626 | 1 |
| mapping | Gleb Belov | These are the models from MiniZinc Challenges 2012-2016 (see www.minizinc.org), compiled for MIP WITH INDICATOR CONSTRAINTS using the develop branch of MiniZinc and CPLEX 12.7.1 on 30 April 2017. Thus, these models can only be handled by solvers accepting indicator constraints. For models compiled with big-M/domain decomposition only, see my previous submission to MIPLIB.To recompile, create a directory MODELS, a list lst12_16.txt of the models with full paths to mzn/dzn files of each model per line, and say$> ~/install/libmzn/tests/benchmarking/mzn-test.py -l ../lst12_16.txt -slvPrf MZN-CPLEX -debug 1 -addOption "-timeout 3 -D fIndConstr=true -D fMIPdomains=false" -useJoinedName "-writeModel MODELS_IND/%s.mps" Alternatively, you can compile individual model as follows: $> mzn-cplex -v -s -G linear -output-time ../challenge_2012_2016/mznc2016_probs/zephyrus/zephyrus.mzn ../challenge_2012_2016/mznc2016_p/zephyrus/14__8__6__3.dzn -a -timeout 3 -D fIndConstr=true -D fMIPdomains=false -writeModel MODELS_IND/challenge_2012_2016mznc2016_probszephyruszephyrusmzn-challenge_2012_2016mznc2016_probszephyrus14__8__6__3dzn.mps | 1.425115 | 2 | |
| allcolor | Domenico Salvagnin | Prepack optimization model. | 1.458631 | 3 | |
| noip | Christopher Hojny | integer programming formulation that verifies that no integer programming formulation of a given 0/1-point set exists | 1.475963 | 4 | |
| sp_product | MIPLIB submission pool | Imported from the MIPLIB2010 submissions. | 1.518820 | 5 |

