gmut-76-50: Instance-to-Instance Comparison Results

Type: Instance
Submitter: Nora Konnyu
Description: Timber harvest scheduling model These are harvest scheduling models of hypothetical forest planning problems where net timber revenues are maximized over a planning horizon subject to four sets of constraints: 1. Each management unit can be harvested only once over the planning horizon, 2. Volume harvested in one planning period should not be less or more than some portion of that in the preceding period, 3. Area-weighted average age of the forest by the end of the plan should notbe less than a certain target age. 4. Clearcut size in any planning period has to be below a specific limit. Decision variable are management units and generalized management units (group of management units with a combined area not exceeding the limit on clearcut size) and can be either fully harvested or left untouched in any planning period, therefore there is a binary restriction on the decision variables.
MIPLIB Entry

Parent Instance (gmut-76-50)

All other instances below were be compared against this "query" instance.

gmut-76-50 Raw gmut-76-50 Decomposed gmut-76-50 Composite of MIC top 5 gmut-76-50 Composite of MIPLIB top 5 gmut-76-50 Model Group Composite
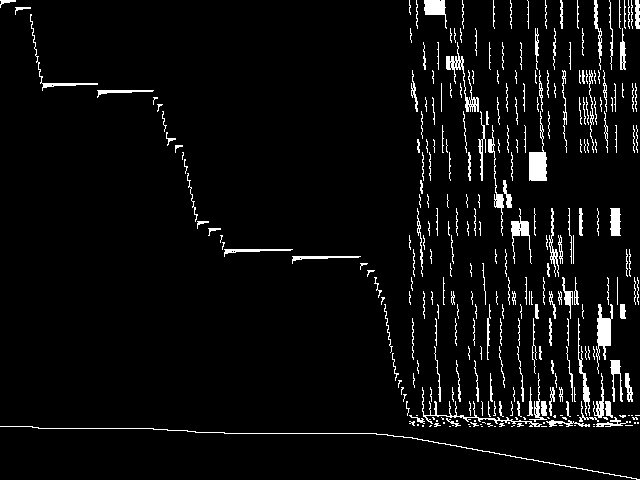
Raw This is the CCM image before the decomposition procedure has been applied.
Decomposed This is the CCM image after a decomposition procedure has been applied. This is the image used by the MIC's image-based comparisons for this query instance.
Composite of MIC Top 5 Composite of the five decomposed CCM images from the MIC Top 5.
Composite of MIPLIB Top 5 Composite of the five decomposed CCM images from the MIPLIB Top 5.
Model Group Composite Image Composite of the decomposed CCM images for every instance in the same model group as this query.

MIC Top 5 Instances

These are the 5 decomposed CCM images that are most similar to decomposed CCM image for the the query instance, according to the ISS metric.

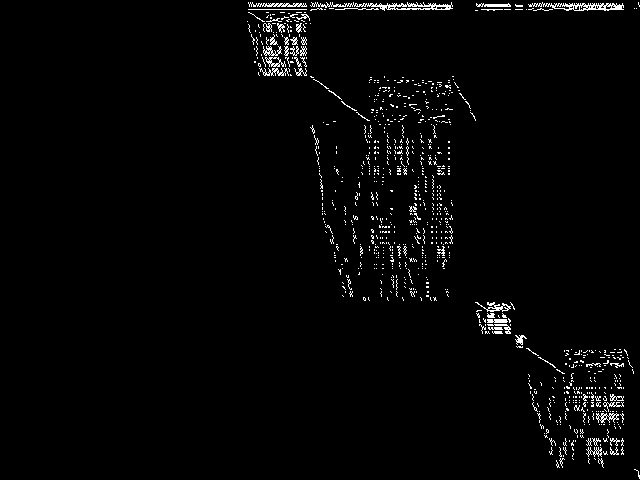
Decomposed These decomposed images were created by GCG.
gmut-76-40 decomposed gmut-75-50 decomposed n2seq36q decomposed rwth-timetable decomposed tpl-tub-ws1617 decomposed
Name gmut-76-40 [MIPLIB] gmut-75-50 [MIPLIB] n2seq36q [MIPLIB] rwth-timetable [MIPLIB] tpl-tub-ws1617 [MIPLIB]
Rank / ISS The image-based structural similarity (ISS) metric measures the Euclidean distance between the image-based feature vectors for the query instance and all other instances. A smaller ISS value indicates greater similarity.
1 / 0.999 2 / 1.212 3 / 1.664 4 / 1.746 5 / 1.816
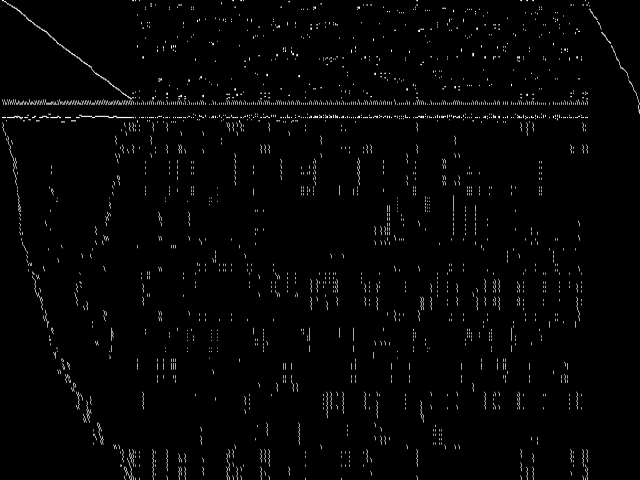
Raw These images represent the CCM images in their raw forms (before any decomposition was applied) for the MIC top 5.
gmut-76-40 raw gmut-75-50 raw n2seq36q raw rwth-timetable raw tpl-tub-ws1617 raw

MIPLIB Top 5 Instances

These are the 5 instances that are most closely related to the query instance, according to the instance statistic-based similarity measure employed by MIPLIB 2017

Decomposed These decomposed images were created by GCG.
gmut-76-40 decomposed gmut-75-50 decomposed gmu-35-50 decomposed gmu-35-40 decomposed supportcase31 decomposed
Name gmut-76-40 [MIPLIB] gmut-75-50 [MIPLIB] gmu-35-50 [MIPLIB] gmu-35-40 [MIPLIB] supportcase31 [MIPLIB]
Rank / ISS The image-based structural similarity (ISS) metric measures the Euclidean distance between the image-based feature vectors for the query instance and all model groups. A smaller ISS value indicates greater similarity.
1 / 0.999 2 / 1.212 84 / 2.640 196 / 2.805 777 / 3.147
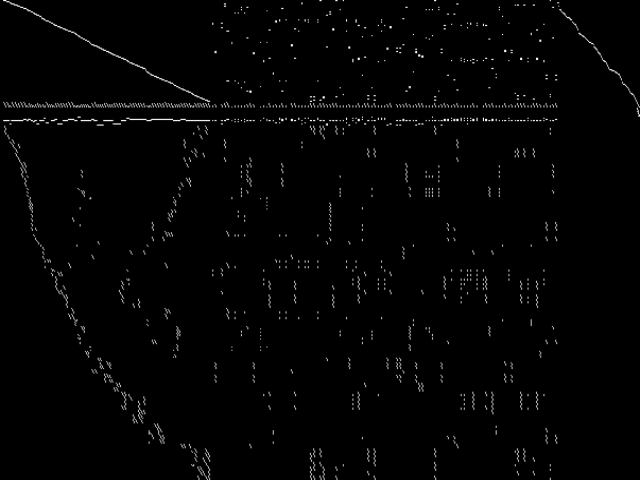
Raw These images represent the CCM images in their raw forms (before any decomposition was applied) for the MIPLIB top 5.
gmut-76-40 raw gmut-75-50 raw gmu-35-50 raw gmu-35-40 raw supportcase31 raw

Instance Summary

The table below contains summary information for gmut-76-50, the five most similar instances to gmut-76-50 according to the MIC, and the five most similar instances to gmut-76-50 according to MIPLIB 2017.

INSTANCE SUBMITTER DESCRIPTION ISS RANK
Parent Instance gmut-76-50 [MIPLIB] Nora Konnyu Timber harvest scheduling model These are harvest scheduling models of hypothetical forest planning problems where net timber revenues are maximized over a planning horizon subject to four sets of constraints: 1. Each management unit can be harvested only once over the planning horizon, 2. Volume harvested in one planning period should not be less or more than some portion of that in the preceding period, 3. Area-weighted average age of the forest by the end of the plan should notbe less than a certain target age. 4. Clearcut size in any planning period has to be below a specific limit. Decision variable are management units and generalized management units (group of management units with a combined area not exceeding the limit on clearcut size) and can be either fully harvested or left untouched in any planning period, therefore there is a binary restriction on the decision variables. 0.000000 -
MIC Top 5 gmut-76-40 [MIPLIB] Nora Konnyu Timber harvest scheduling model These are harvest scheduling models of hypothetical forest planning problems where net timber revenues are maximized over a planning horizon subject to four sets of constraints: 1. Each management unit can be harvested only once over the planning horizon, 2. Volume harvested in one planning period should not be less or more than some portion of that in the preceding period, 3. Area-weighted average age of the forest by the end of the plan should notbe less than a certain target age. 4. Clearcut size in any planning period has to be below a specific limit. Decision variable are management units and generalized management units (group of management units with a combined area not exceeding the limit on clearcut size) and can be either fully harvested or left untouched in any planning period, therefore there is a binary restriction on the decision variables. 0.999458 1
gmut-75-50 [MIPLIB] Nora Konnyu Timber harvest scheduling model. Solved by ParaXpress in a 12288 core supercomputer run on HLRN III. These are harvest scheduling models of hypothetical forest planning problems where net timber revenues are maximized over a planning horizon subject to four sets of constraints: 1. Each management unit can be harvested only once over the planning horizon, 2. Volume harvested in one planning period should not be less or more than some portion of that in the preceding period, 3. Area-weighted average age of the forest by the end of the plan should notbe less than a certain target age. 4. Clearcut size in any planning period has to be below a specific limit. Decision variable are management units and generalized management units (group of management units with a combined area not exceeding the limit on clearcut size) and can be either fully harvested or left untouched in any planning period, therefore there is a binary restriction on the decision variables. 1.211727 2
n2seq36q [MIPLIB] R. Meirich Static line planning models on the Dutch IC network 1.664160 3
rwth-timetable [MIPLIB] Gerald Lach University Course Timetabling from the RWTH Aachen 1.746082 4
tpl-tub-ws1617 [MIPLIB] János Höner Model for the Post-Enrollment Course Timetabling Problem at TU Berlin from the summer term 2016 and the winter term 2016/2017 1.816223 5
MIPLIB Top 5 gmut-76-40 [MIPLIB] Nora Konnyu Timber harvest scheduling model These are harvest scheduling models of hypothetical forest planning problems where net timber revenues are maximized over a planning horizon subject to four sets of constraints: 1. Each management unit can be harvested only once over the planning horizon, 2. Volume harvested in one planning period should not be less or more than some portion of that in the preceding period, 3. Area-weighted average age of the forest by the end of the plan should notbe less than a certain target age. 4. Clearcut size in any planning period has to be below a specific limit. Decision variable are management units and generalized management units (group of management units with a combined area not exceeding the limit on clearcut size) and can be either fully harvested or left untouched in any planning period, therefore there is a binary restriction on the decision variables. 0.999458 1
gmut-75-50 [MIPLIB] Nora Konnyu Timber harvest scheduling model. Solved by ParaXpress in a 12288 core supercomputer run on HLRN III. These are harvest scheduling models of hypothetical forest planning problems where net timber revenues are maximized over a planning horizon subject to four sets of constraints: 1. Each management unit can be harvested only once over the planning horizon, 2. Volume harvested in one planning period should not be less or more than some portion of that in the preceding period, 3. Area-weighted average age of the forest by the end of the plan should notbe less than a certain target age. 4. Clearcut size in any planning period has to be below a specific limit. Decision variable are management units and generalized management units (group of management units with a combined area not exceeding the limit on clearcut size) and can be either fully harvested or left untouched in any planning period, therefore there is a binary restriction on the decision variables. 1.211727 2
gmu-35-50 [MIPLIB] Nora Konnyu Timber harvest scheduling model These are harvest scheduling models of hypothetical forest planning problems where net timber revenues are maximized over a planning horizon subject to four sets of constraints: 1. Each management unit can be harvested only once over the planning horizon, 2. Volume harvested in one planning period should not be less or more than some portion of that in the preceding period, 3. Area-weighted average age of the forest by the end of the plan should notbe less than a certain target age. 4. Clearcut size in any planning period has to be below a specific limit. Decision variable are management units and generalized management units (group of management units with a combined area not exceeding the limit on clearcut size) and can be either fully harvested or left untouched in any planning period, therefore there is a binary restriction on the decision variables. 2.639525 84
gmu-35-40 [MIPLIB] Nora Konnyu Timber harvest scheduling model These are harvest scheduling models of hypothetical forest planning problems where net timber revenues are maximized over a planning horizon subject to four sets of constraints: 1. Each management unit can be harvested only once over the planning horizon, 2. Volume harvested in one planning period should not be less or more than some portion of that in the preceding period, 3. Area-weighted average age of the forest by the end of the plan should notbe less than a certain target age. 4. Clearcut size in any planning period has to be below a specific limit. Decision variable are management units and generalized management units (group of management units with a combined area not exceeding the limit on clearcut size) and can be either fully harvested or left untouched in any planning period, therefore there is a binary restriction on the decision variables. 2.804912 196
supportcase31 [MIPLIB] Domenico Salvagnin Instance coming from IBM developerWorks forum with unknown application. 3.146931 777


gmut-76-50: Instance-to-Model Comparison Results

Model Group Assignment from MIPLIB: gmu
Assigned Model Group Rank/ISS in the MIC: 1 / 1.924

MIC Top 5 Model Groups

These are the 5 model group composite (MGC) images that are most similar to the decomposed CCM image for the query instance, according to the ISS metric.

These are model group composite (MGC) images for the MIC top 5 model groups.
Model group: gmu Model group: neos-pseudoapplication-49 Model group: maxfeassub Model group: momentum Model group: cryptanalysis
Name gmu neos-pseudoapplication-49 maxfeassub momentum cryptanalysis
Rank / ISS The image-based structural similarity (ISS) metric measures the Euclidean distance between the image-based feature vectors for the query instance and all other instances. A smaller ISS value indicates greater similarity.
1 / 1.925 2 / 2.537 3 / 2.658 4 / 2.687 5 / 2.702

Model Group Summary

The table below contains summary information for the five most similar model groups to gmut-76-50 according to the MIC.

MODEL GROUP SUBMITTER DESCRIPTION ISS RANK
MIC Top 5 gmu Nora Konnyu Timber harvest scheduling model These are harvest scheduling models of hypothetical forest planning problems where net timber revenues are maximized over a planning horizon subject to four sets of constraints: 1. Each management unit can be harvested only once over the planning horizon, 2. Volume harvested in one planning period should not be less or more than some portion of that in the preceding period, 3. Area-weighted average age of the forest by the end of the plan should notbe less than a certain target age. 4. Clearcut size in any planning period has to be below a specific limit. Decision variable are management units and generalized management units (group of management units with a combined area not exceeding the limit on clearcut size) and can be either fully harvested or left untouched in any planning period, therefore there is a binary restriction on the decision variables. 1.924784 1
neos-pseudoapplication-49 NEOS Server Submission Imported from the MIPLIB2010 submissions. 2.537259 2
maxfeassub Marc Pfetsch Set covering problems arising from a Benders algorithm for finding maximum feasible subsystems. More details on the generation is given in the README file in the tarball. 2.658383 3
momentum T. Koch Snapshot based UMTS planning problem, having a very wide dynamic range in the matrix coefficients and tending to be numerically unstable. Solved with Gurobi 4.5.1 on a 12-core Linux system in 3590.41 sec. 2.686899 4
cryptanalysis Gleb Belov Linearized Constraint Programming models of the MiniZinc Challenges 2012-2016. I should be able to produce versions with indicator constraints supported by Gurobi and CPLEX, however don't know if you can use them and if there is a standard format. These MPS were produced by Gurobi 7.0.2 using the MiniZinc develop branch on eb536656062ca13325a96b5d0881742c7d0e3c38 2.701939 5


Updated August 16, 2019