Instance - gsvm2rl12

gsvm2rl12: Instance-to-Instance Comparison Results

Type:	Instance
Submitter:	Toni Sorrell
Description:	Suport vector machine with ramp loss. GSVM2-RL is the formulation found in Hess E. and Brooks P. (2015) paper, The Support Vector Machine and Mixed Integer Linear Programming: Ramp Loss SVM with L1-Norm Regularization
	MIPLIB Entry


	Raw This is the CCM image before the decomposition procedure has been applied.	Decomposed This is the CCM image after a decomposition procedure has been applied. This is the image used by the MIC's image-based comparisons for this query instance.	Composite of MIC Top 5 Composite of the five decomposed CCM images from the MIC Top 5.	Composite of MIPLIB Top 5 Composite of the five decomposed CCM images from the MIPLIB Top 5.	Model Group Composite Image Composite of the decomposed CCM images for every instance in the same model group as this query.

Decomposed These decomposed images were created by GCG.
Name	gsvm2rl3 [MIPLIB]	gsvm2rl5 [MIPLIB]	mik-250-20-75-5 [MIPLIB]	gsvm2rl9 [MIPLIB]	square37 [MIPLIB]
Rank / ISS The image-based structural similarity (ISS) metric measures the Euclidean distance between the image-based feature vectors for the query instance and all other instances. A smaller ISS value indicates greater similarity.	1 / 0.358	2 / 0.505	3 / 0.635	4 / 0.776	5 / 0.828
Raw These images represent the CCM images in their raw forms (before any decomposition was applied) for the MIC top 5.

Decomposed These decomposed images were created by GCG.
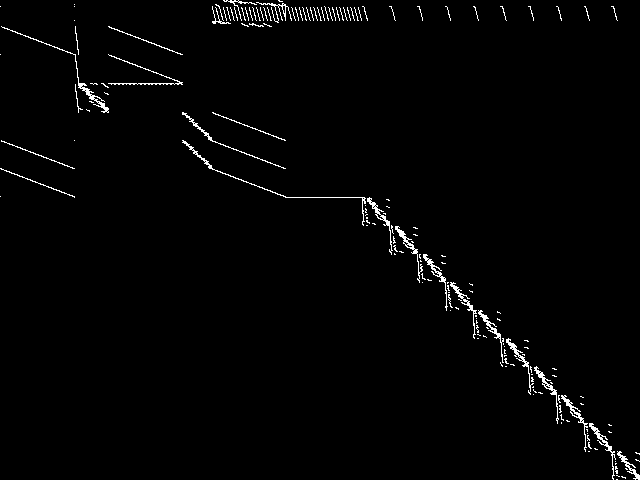Name	gsvm2rl3 [MIPLIB]	gsvm2rl5 [MIPLIB]	gsvm2rl9 [MIPLIB]	neos-619167 [MIPLIB]	gsvm2rl11* [MIPLIB]
Rank / ISS The image-based structural similarity (ISS) metric measures the Euclidean distance between the image-based feature vectors for the query instance and all model groups. A smaller ISS value indicates greater similarity.	1 / 0.358	2 / 0.505	4 / 0.776	274 / 1.235	0* / 0.000*
Raw These images represent the CCM images in their raw forms (before any decomposition was applied) for the MIPLIB top 5.

Instance Summary

The table below contains summary information for gsvm2rl12, the five most similar instances to gsvm2rl12 according to the MIC, and the five most similar instances to gsvm2rl12 according to MIPLIB 2017.

	INSTANCE	SUBMITTER	DESCRIPTION	ISS	RANK
Parent Instance	gsvm2rl12 [MIPLIB]	Toni Sorrell	Suport vector machine with ramp loss. GSVM2-RL is the formulation found in Hess E. and Brooks P. (2015) paper, The Support Vector Machine and Mixed Integer Linear Programming: Ramp Loss SVM with L1-Norm Regularization	0.000000	-
MIC Top 5	gsvm2rl3 [MIPLIB]	Toni Sorrell	Suport vector machine with ramp loss. GSVM2-RL is the formulation found in Hess E. and Brooks P. (2015) paper, The Support Vector Machine and Mixed Integer Linear Programming: Ramp Loss SVM with L1-Norm Regularization	0.357644	1
	gsvm2rl5 [MIPLIB]	Toni Sorrell	Suport vector machine with ramp loss. GSVM2-RL is the formulation found in Hess E. and Brooks P. (2015) paper, The Support Vector Machine and Mixed Integer Linear Programming: Ramp Loss SVM with L1-Norm Regularization	0.504636	2
	mik-250-20-75-5 [MIPLIB]	MIPLIB submission pool	Imported from the MIPLIB2010 submissions.	0.634940	3
	gsvm2rl9 [MIPLIB]	Toni Sorrell	Suport vector machine with ramp loss. GSVM2-RL is the formulation found in Hess E. and Brooks P. (2015) paper, The Support Vector Machine and Mixed Integer Linear Programming: Ramp Loss SVM with L1-Norm Regularization	0.776453	4
	square37 [MIPLIB]	Sascha Kurz	Squaring the square For a given integer n, determine the minimum number of squares in a tiling of an \\(n\\times n\\) square using using only integer sided squares of smaller size. (Although the models get quite large even for moderate n, they can be solved to optimality for all \\(n \\le 61\\), while challenging the MIP solver, especially the presolver.)	0.828078	5
MIPLIB Top 5	gsvm2rl3 [MIPLIB]	Toni Sorrell	Suport vector machine with ramp loss. GSVM2-RL is the formulation found in Hess E. and Brooks P. (2015) paper, The Support Vector Machine and Mixed Integer Linear Programming: Ramp Loss SVM with L1-Norm Regularization	0.357644	1
	gsvm2rl5 [MIPLIB]	Toni Sorrell	Suport vector machine with ramp loss. GSVM2-RL is the formulation found in Hess E. and Brooks P. (2015) paper, The Support Vector Machine and Mixed Integer Linear Programming: Ramp Loss SVM with L1-Norm Regularization	0.504636	2
	gsvm2rl9 [MIPLIB]	Toni Sorrell	Suport vector machine with ramp loss. GSVM2-RL is the formulation found in Hess E. and Brooks P. (2015) paper, The Support Vector Machine and Mixed Integer Linear Programming: Ramp Loss SVM with L1-Norm Regularization	0.776453	4
	neos-619167 [MIPLIB]	NEOS Server Submission	Imported from the MIPLIB2010 submissions.	1.234571	274
	gsvm2rl11* [MIPLIB]	Toni Sorrell	Suport vector machine with ramp loss. GSVM2-RL is the formulation found in Hess E. and Brooks P. (2015) paper, The Support Vector Machine and Mixed Integer Linear Programming: Ramp Loss SVM with L1-Norm Regularization	0.000000*	0*

gsvm2rl12: Instance-to-Model Comparison Results

Model Group Assignment from MIPLIB:	supportvectormachine
Assigned Model Group Rank/ISS in the MIC:	1 / 0.277

These are model group composite (MGC) images for the MIC top 5 model groups.
Name	supportvectormachine	square	neos-pseudoapplication-74	neos-pseudoapplication-2	scp
Rank / ISS The image-based structural similarity (ISS) metric measures the Euclidean distance between the image-based feature vectors for the query instance and all other instances. A smaller ISS value indicates greater similarity.	1 / 0.277	2 / 1.366	3 / 1.392	4 / 1.436	5 / 1.442

Model Group Summary

The table below contains summary information for the five most similar model groups to gsvm2rl12 according to the MIC.

	MODEL GROUP	SUBMITTER	DESCRIPTION	ISS	RANK
MIC Top 5	supportvectormachine	Toni Sorrell	Suport vector machine with ramp loss. GSVM2-RL is the formulation found in Hess E. and Brooks P. (2015) paper, The Support Vector Machine and Mixed Integer Linear Programming: Ramp Loss SVM with L1-Norm Regularization	0.277233	1
	square	Sascha Kurz	Squaring the square For a given integer n, determine the minimum number of squares in a tiling of an \\(n\\times n\\) square using using only integer sided squares of smaller size. (Although the models get quite large even for moderate n, they can be solved to optimality for all \\(n \\le 61\\), while challenging the MIP solver, especially the presolver.)	1.366456	2
	neos-pseudoapplication-74	Jeff Linderoth	(None provided)	1.392365	3
	neos-pseudoapplication-2	NEOS Server Submission	Imported from the MIPLIB2010 submissions.	1.435838	4
	scp	Shunji Umetani	This is a random test model generator for SCP using the scheme of the following paper, namely the column cost c[j] are integer randomly generated from [1,100]; every column covers at least one row; and every row is covered by at least two columns. see reference: E. Balas and A. Ho, Set covering algorithms using cutting planes, heuristics, and subgradient optimization: A computational study, Mathematical Programming, 12 (1980), 37-60. We have newly generated Classes I-N with the following parameter values, where each class has five models. We have also generated reduced models by a standard pricing method in the following paper: S. Umetani and M. Yagiura, Relaxation heuristics for the set covering problem, Journal of the Operations Research Society of Japan, 50 (2007), 350-375. You can obtain the model generator program from the following web site. https://sites.google.com/site/shunjiumetani/benchmark	1.441647	5

gsvm2rl12: Instance-to-Instance Comparison Results

Parent Instance (gsvm2rl12)

MIC Top 5 Instances

MIPLIB Top 5 Instances

Instance Summary

gsvm2rl12: Instance-to-Model Comparison Results

MIC Top 5 Model Groups

Model Group Summary