×
![]()
gsvm2rl3: Instance-to-Instance Comparison Results
| Type: | Instance |
| Submitter: | Toni Sorrell |
| Description: | Suport vector machine with ramp loss. GSVM2-RL is the formulation found in Hess E. and Brooks P. (2015) paper, The Support Vector Machine and Mixed Integer Linear Programming: Ramp Loss SVM with L1-Norm Regularization |
| MIPLIB Entry |
Parent Instance (gsvm2rl3)
All other instances below were be compared against this "query" instance.  |
 |
 |
 |
 |
 |
|
Raw
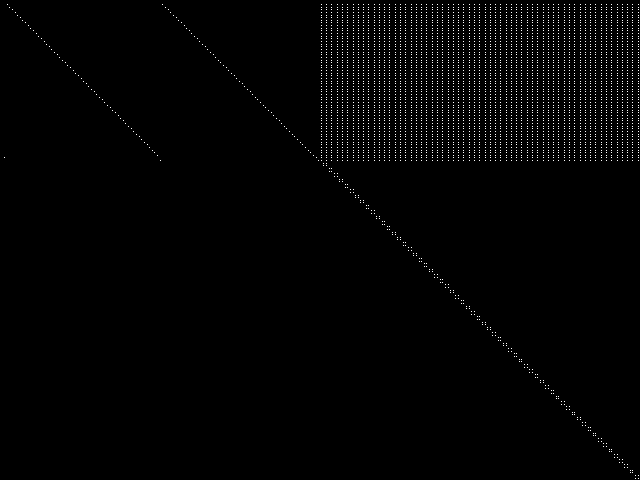
This is the CCM image before the decomposition procedure has been applied.
|
Decomposed
This is the CCM image after a decomposition procedure has been applied. This is the image used by the MIC's image-based comparisons for this query instance.
|
Composite of MIC Top 5
Composite of the five decomposed CCM images from the MIC Top 5.
|
Composite of MIPLIB Top 5
Composite of the five decomposed CCM images from the MIPLIB Top 5.
|
Model Group Composite Image
Composite of the decomposed CCM images for every instance in the same model group as this query.
|
MIC Top 5 Instances
These are the 5 decomposed CCM images that are most similar to decomposed CCM image for the the query instance, according to the ISS metric.  |
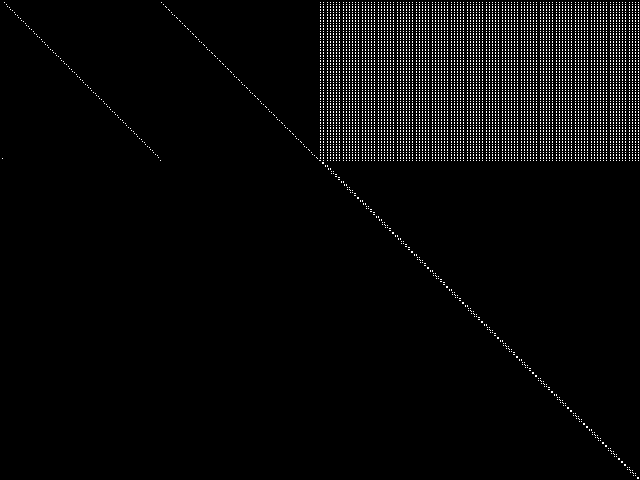
Decomposed
These decomposed images were created by GCG.
|
 |
 |
 |
 |
 |
| Name | gsvm2rl12 [MIPLIB] | gsvm2rl5 [MIPLIB] | mik-250-20-75-5 [MIPLIB] | gsvm2rl9 [MIPLIB] | square37 [MIPLIB] | |
|
Rank / ISS
The image-based structural similarity (ISS) metric measures the Euclidean distance between the image-based feature vectors for the query instance and all other instances. A smaller ISS value indicates greater similarity.
|
1 / 0.358 | 2 / 0.422 | 3 / 0.596 | 4 / 0.728 | 5 / 0.774 | |
|
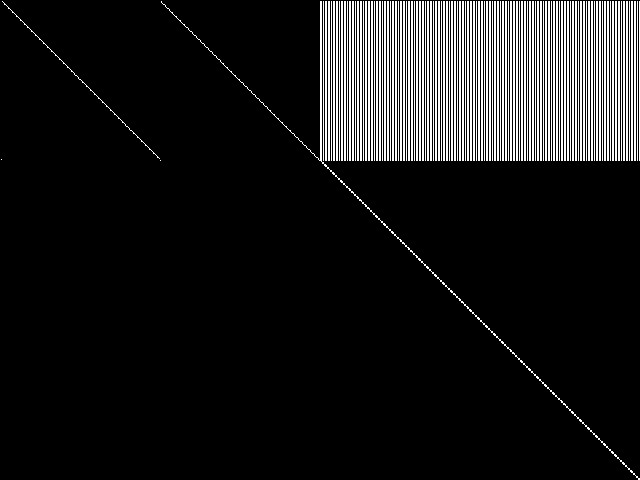
Raw
These images represent the CCM images in their raw forms (before any decomposition was applied) for the MIC top 5.
|
 |
 |
 |
 |
 |
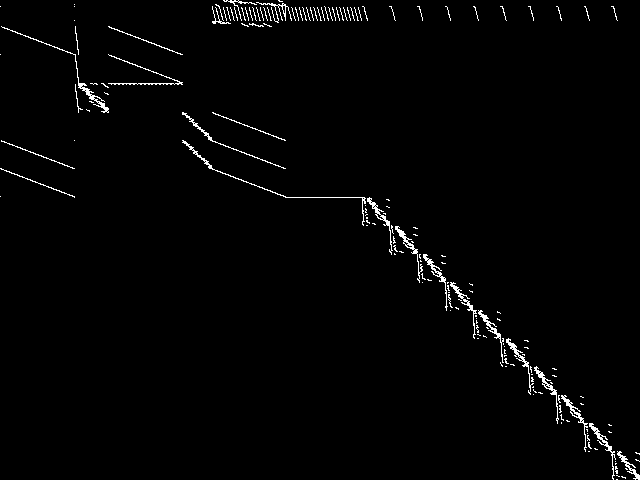
MIPLIB Top 5 Instances
These are the 5 instances that are most closely related to the query instance, according to the instance statistic-based similarity measure employed by MIPLIB 2017  |
Decomposed
These decomposed images were created by GCG.
|
 |
 |
 |
 |
 |
| Name | gsvm2rl12 [MIPLIB] | gsvm2rl5 [MIPLIB] | gsvm2rl9 [MIPLIB] | neos-619167 [MIPLIB] | gsvm2rl11* [MIPLIB] | |
|
Rank / ISS
The image-based structural similarity (ISS) metric measures the Euclidean distance between the image-based feature vectors for the query instance and all model groups. A smaller ISS value indicates greater similarity.
|
1 / 0.358 | 2 / 0.422 | 4 / 0.728 | 279 / 1.220 | 1* / 0.358* | |
|
Raw
These images represent the CCM images in their raw forms (before any decomposition was applied) for the MIPLIB top 5.
|
 |
 |
 |
 |
 |
Instance Summary
The table below contains summary information for gsvm2rl3, the five most similar instances to gsvm2rl3 according to the MIC, and the five most similar instances to gsvm2rl3 according to MIPLIB 2017.
| INSTANCE | SUBMITTER | DESCRIPTION | ISS | RANK | |
|---|---|---|---|---|---|
| Parent Instance | gsvm2rl3 [MIPLIB] | Toni Sorrell | Suport vector machine with ramp loss. GSVM2-RL is the formulation found in Hess E. and Brooks P. (2015) paper, The Support Vector Machine and Mixed Integer Linear Programming: Ramp Loss SVM with L1-Norm Regularization | 0.000000 | - |
| MIC Top 5 | gsvm2rl12 [MIPLIB] | Toni Sorrell | Suport vector machine with ramp loss. GSVM2-RL is the formulation found in Hess E. and Brooks P. (2015) paper, The Support Vector Machine and Mixed Integer Linear Programming: Ramp Loss SVM with L1-Norm Regularization | 0.357644 | 1 |
| gsvm2rl5 [MIPLIB] | Toni Sorrell | Suport vector machine with ramp loss. GSVM2-RL is the formulation found in Hess E. and Brooks P. (2015) paper, The Support Vector Machine and Mixed Integer Linear Programming: Ramp Loss SVM with L1-Norm Regularization | 0.421542 | 2 | |
| mik-250-20-75-5 [MIPLIB] | MIPLIB submission pool | Imported from the MIPLIB2010 submissions. | 0.596051 | 3 | |
| gsvm2rl9 [MIPLIB] | Toni Sorrell | Suport vector machine with ramp loss. GSVM2-RL is the formulation found in Hess E. and Brooks P. (2015) paper, The Support Vector Machine and Mixed Integer Linear Programming: Ramp Loss SVM with L1-Norm Regularization | 0.728377 | 4 | |
| square37 [MIPLIB] | Sascha Kurz | Squaring the square For a given integer n, determine the minimum number of squares in a tiling of an \\(n\\times n\\) square using using only integer sided squares of smaller size. (Although the models get quite large even for moderate n, they can be solved to optimality for all \\(n \\le 61\\), while challenging the MIP solver, especially the presolver.) | 0.774305 | 5 | |
| MIPLIB Top 5 | gsvm2rl12 [MIPLIB] | Toni Sorrell | Suport vector machine with ramp loss. GSVM2-RL is the formulation found in Hess E. and Brooks P. (2015) paper, The Support Vector Machine and Mixed Integer Linear Programming: Ramp Loss SVM with L1-Norm Regularization | 0.357644 | 1 |
| gsvm2rl5 [MIPLIB] | Toni Sorrell | Suport vector machine with ramp loss. GSVM2-RL is the formulation found in Hess E. and Brooks P. (2015) paper, The Support Vector Machine and Mixed Integer Linear Programming: Ramp Loss SVM with L1-Norm Regularization | 0.421542 | 2 | |
| gsvm2rl9 [MIPLIB] | Toni Sorrell | Suport vector machine with ramp loss. GSVM2-RL is the formulation found in Hess E. and Brooks P. (2015) paper, The Support Vector Machine and Mixed Integer Linear Programming: Ramp Loss SVM with L1-Norm Regularization | 0.728377 | 4 | |
| neos-619167 [MIPLIB] | NEOS Server Submission | Imported from the MIPLIB2010 submissions. | 1.220367 | 279 | |
| gsvm2rl11* [MIPLIB] | Toni Sorrell | Suport vector machine with ramp loss. GSVM2-RL is the formulation found in Hess E. and Brooks P. (2015) paper, The Support Vector Machine and Mixed Integer Linear Programming: Ramp Loss SVM with L1-Norm Regularization | 0.357644* | 1* |
gsvm2rl3: Instance-to-Model Comparison Results
| Model Group Assignment from MIPLIB: | supportvectormachine |
| Assigned Model Group Rank/ISS in the MIC: | 1 / 1.006 |
MIC Top 5 Model Groups
These are the 5 model group composite (MGC) images that are most similar to the decomposed CCM image for the query instance, according to the ISS metric.  |
These are model group composite (MGC) images for the MIC top 5 model groups.
|
 |
 |
 |
 |
 |
| Name | supportvectormachine | mik_250 | bc | scp | square | |
|
Rank / ISS
The image-based structural similarity (ISS) metric measures the Euclidean distance between the image-based feature vectors for the query instance and all other instances. A smaller ISS value indicates greater similarity.
|
1 / 1.007 | 2 / 1.175 | 3 / 1.649 | 4 / 1.733 | 5 / 1.744 |
Model Group Summary
The table below contains summary information for the five most similar model groups to gsvm2rl3 according to the MIC.
| MODEL GROUP | SUBMITTER | DESCRIPTION | ISS | RANK | |
|---|---|---|---|---|---|
| MIC Top 5 | supportvectormachine | Toni Sorrell | Suport vector machine with ramp loss. GSVM2-RL is the formulation found in Hess E. and Brooks P. (2015) paper, The Support Vector Machine and Mixed Integer Linear Programming: Ramp Loss SVM with L1-Norm Regularization | 1.006652 | 1 |
| mik_250 | MIPLIB submission pool | Imported from the MIPLIB2010 submissions. | 1.174999 | 2 | |
| bc | MIPLIB submission pool | Imported from the MIPLIB2010 submissions. | 1.648711 | 3 | |
| scp | Shunji Umetani | This is a random test model generator for SCP using the scheme of the following paper, namely the column cost c[j] are integer randomly generated from [1,100]; every column covers at least one row; and every row is covered by at least two columns. see reference: E. Balas and A. Ho, Set covering algorithms using cutting planes, heuristics, and subgradient optimization: A computational study, Mathematical Programming, 12 (1980), 37-60. We have newly generated Classes I-N with the following parameter values, where each class has five models. We have also generated reduced models by a standard pricing method in the following paper: S. Umetani and M. Yagiura, Relaxation heuristics for the set covering problem, Journal of the Operations Research Society of Japan, 50 (2007), 350-375. You can obtain the model generator program from the following web site. https://sites.google.com/site/shunjiumetani/benchmark | 1.733059 | 4 | |
| square | Sascha Kurz | Squaring the square For a given integer n, determine the minimum number of squares in a tiling of an \\(n\\times n\\) square using using only integer sided squares of smaller size. (Although the models get quite large even for moderate n, they can be solved to optimality for all \\(n \\le 61\\), while challenging the MIP solver, especially the presolver.) | 1.744168 | 5 |

